详解准确率、精确率、召回率、F1值等评价指标的含义

大家好，欢迎来到IT知识分享网。

机器学习问题之中，通常需要建立模型来解决具体问题，但对于模型的好坏，也就是模型的泛化能力，如何进行评估呢？

很简单，我们可以定一些评价指标，来度量模型的优劣。比如准确率、精确率、召回率、F1值、ROC、AUC等指标，但是你清楚这些指标的具体含义吗？下面我们一起来看看吧。

1.混淆矩阵

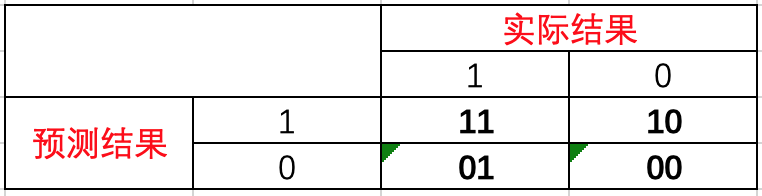
介绍各个指标之前，我们先来了解一下混淆矩阵。假如现在有一个二分类问题，那么预测结果和实际结果两两结合会出现如下四种情况。

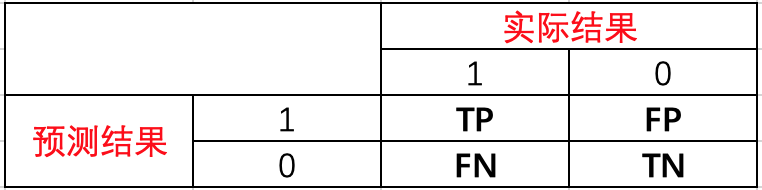
由于用数字1、0表示不太方便阅读，我们转换一下，用T(True)代表正确、F(False)代表错误、P(Positive)代表1、N(Negative)代表0。先看预测结果(P|N)，然后再针对实际结果对比预测结果，给出判断结果(T|F)。按照上面逻辑，重新分配后为

TP、FP、FN、TN可以理解为

• TP：预测为1，实际为1，预测正确。
• FP：预测为1，实际为0，预测错误。
• FN：预测为0，实际为1，预测错误。
• TN：预测为0，实际为0，预测正确。

2.准确率

首先给出准确率(Accuracy) 的定义，即预测正确的结果占总样本的百分比，表达式为
$$准确率=\frac{TP+TN}{TP+TN+FP+FN}$$
虽然准确率能够判断总的正确率，但是在样本不均衡的情况下，并不能作为很好的指标来衡量结果。

比如在样本集中，正样本有90个，负样本有10个，样本是严重的不均衡。对于这种情况，我们只需要将全部样本预测为正样本，就能得到90%的准确率，但是完全没有意义。对于新数据，完全体现不出准确率。因此，在样本不平衡的情况下，得到的高准确率没有任何意义，此时准确率就会失效。所以，我们需要寻找新的指标来评价模型的优劣。

3.精确率

精确率(Precision) 是针对预测结果而言的，其含义是在被所有预测为正的样本中实际为正样本的概率，表达式为
$$精确率=\frac{TP}{TP+FP}$$
精确率和准确率看上去有些类似，但是是两个完全不同的概念。精确率代表对正样本结果中的预测准确程度，准确率则代表整体的预测准确程度，包括正样本和负样本。

4.召回率

召回率(Recall) 是针对原样本而言的，其含义是在实际为正的样本中被预测为正样本的概率，表达式为
$$召回率=\frac{TP}{TP+FN}$$
下面我们通过一个简单例子来看看精确率和召回率。假设一共有10篇文章，里面4篇是你要找的。根据你的算法模型，你找到了5篇，但实际上在这5篇之中，只有3篇是你真正要找的。

那么算法的精确率是3/5=60%，也就是你找的这5篇，有3篇是真正对的。算法的召回率是3/4=75%，也就是需要找的4篇文章，你找到了其中三篇。以精确率还是以召回率作为评价指标，需要根据具体问题而定。

5.F1分数

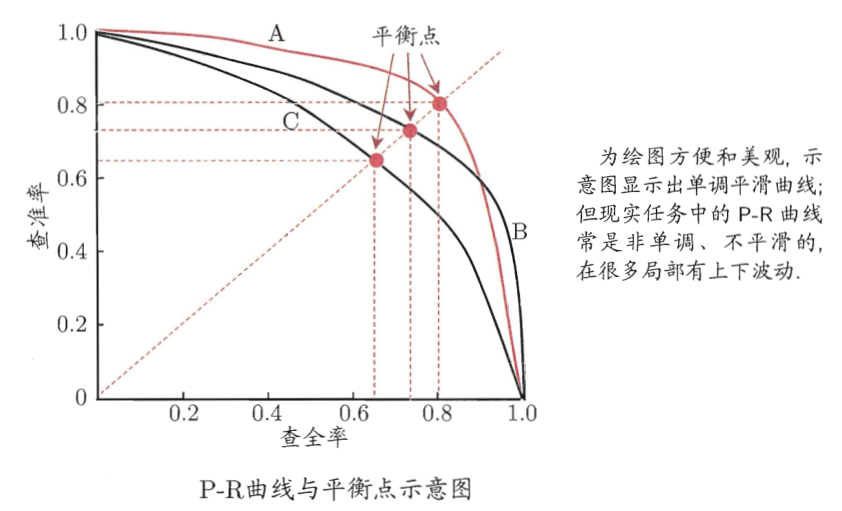
精确率和召回率又被叫做查准率和查全率，可以通过P-R图进行表示

如何理解P-R(精确率-召回率)曲线呢？或者说这些曲线是根据什么变化呢？

以逻辑回归举例，其输出值是0-1之间的数字。因此，如果我们想要判断用户的好坏，那么就必须定一个阈值。比如大于0.5指定为好用户，小于0.5指定为坏用户，然后就可以得到相应的精确率和召回率。但问题是，这个阈值是我们随便定义的，并不知道这个阈值是否符合我们的要求。因此为了寻找一个合适的阈值，我们就需要遍历0-1之间所有的阈值，而每个阈值都对应一个精确率和召回率，从而就能够得到上述曲线。

根据上述的P-R曲线，怎么判断最好的阈值点呢？首先我们先明确目标，我们希望精确率和召回率都很高，但实际上是矛盾的，上述两个指标是矛盾体，无法做到双高。因此，选择合适的阈值点，就需要根据实际问题需求，比如我们想要很高的精确率，就要牺牲掉一些召回率。想要得到很高的召回率，就要牺牲掉一些精准率。但通常情况下，我们可以根据他们之间的平衡点，定义一个新的指标：F1分数(F1-Score)。F1分数同时考虑精确率和召回率，让两者同时达到最高，取得平衡。F1分数表达式为
$$F1分数=\frac{2\ast 精确率\ast 召回率}{精确率+召回率}$$
上图P-R曲线中，平衡点就是F1值的分数。

6.Roc、AUC曲线

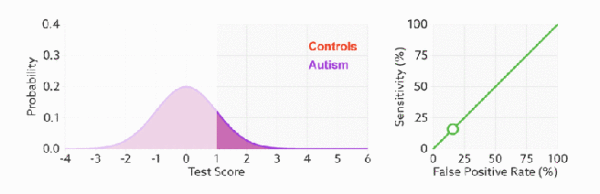
正式介绍ROC和AUC之前，还需要再介绍两个指标，真正率(TPR)和假正率(FPR)。

• 真正率(TPR) = 灵敏度(Sensitivity) = TP/(TP+FN)
• 假正率(FPR) = 1-特异度(Specificity) = FP/(FP+TN)

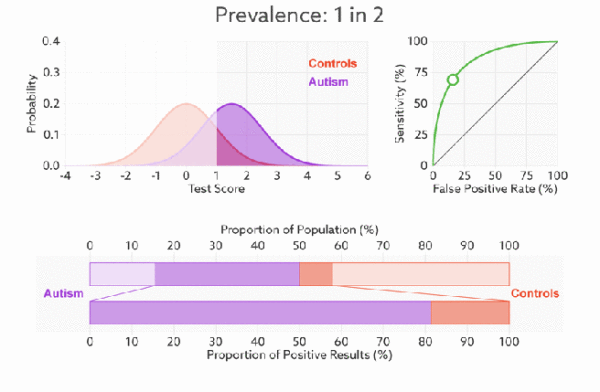
TPR和FPR分别是基于实际表现1、0出发的，也就是说在实际的正样本和负样本中来观察相关概率问题。因此，无论样本是否均衡，都不会被影响。

继续用上面例子，总样本中有90%的正样本，10%的负样本。TPR能够得到90%正样本中有多少是被真正覆盖的，而与那10%无关。同理FPR能够得到10%负样本中有多少是被覆盖的，而与那90%无关。因此我们从实际表现的各个结果出发，就能避免样本不平衡的问题，这就是为什么用TPR和FPR作为ROC、AUC指标的原因。

6.1 ROC

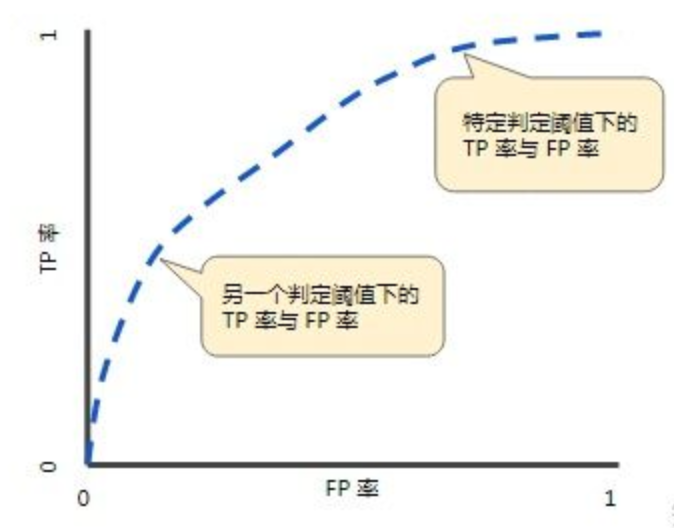
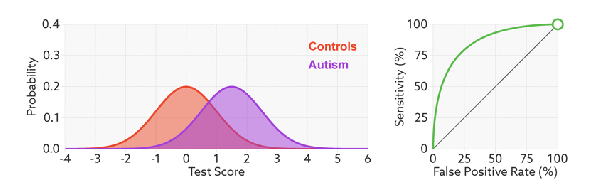
ROC曲线图如下所示，其中横坐标为假正率(FPR)，纵坐标为真正率(TPR)。

与前面的P-R曲线类似，ROC曲线也是通过遍历所有阈值来绘制曲线的。如果我们不断的遍历所有阈值，预测的正样本和负样本是在不断变化的，相应的ROC曲线TPR和FPR也会沿着曲线滑动。

同时，我们也会思考，如何判断ROC曲线的好坏呢？我们来看，FPR表示模型虚报的程度，TPR表示模型预测覆盖的程度。理所当然的，我们希望虚报的越少越好，覆盖的越多越好。所以TPR越高，同时FPR越低，也就是ROC曲线越陡，那么模型的性能也就越好。

最后，我们来看一下，不论样本比例如何改变，ROC曲线都没有影响，也就是ROC曲线无视样本间的不平衡问题。

6.2 AUC

AUC(Area Under Curve) 表示ROC中曲线下的面积，用于判断模型的优劣。如ROC曲线所示，连接对角线的面积刚好是0.5，对角线的含义也就是随机判断预测结果，正负样本覆盖应该都是50%。另外，ROC曲线越陡越好，所以理想值是1，即正方形。所以AUC的值一般是介于0.5和1之间的。AUC评判标准可参考如下

• 0.5-0.7：效果较低。
• 0.7-0.85：效果一般。
• 0.85-0.95：效果很好。
• 0.95-1：效果非常好。

7.推广

更多内容请关注公众号谓之小一，若有疑问可在公众号后台提问，随时回答，欢迎关注，内容转载请注明出处。