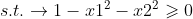大家好,欢迎来到IT知识分享网。
最优化方法
当我们准备好了一个函数表达式之后,如何求解该函数的最优值就会成为一个巨大的挑战。以下是常用的四种优化方法。
无约束优化问题
所谓无约束优化问题,就是指对一个函数求最优值,最优值可以出现在函数上任意一点,而我们不去限定查找最优值的范围。
有约束优化问题
有约束优化问题就是指给自变量的取值范围做限制,缩小优化范围,经典的约束优化算法有:
- 内点法(interior-point)
- 有效集法(active-set)
- SQP算法(sqp)
- 信赖域反射法(trust-region-reflective)
约束,又分线性约束与非线性约束,所谓线性约束,就是指约束条件中的自变量都是1次幂的,非线性约束即有高次幂的自变量出现。
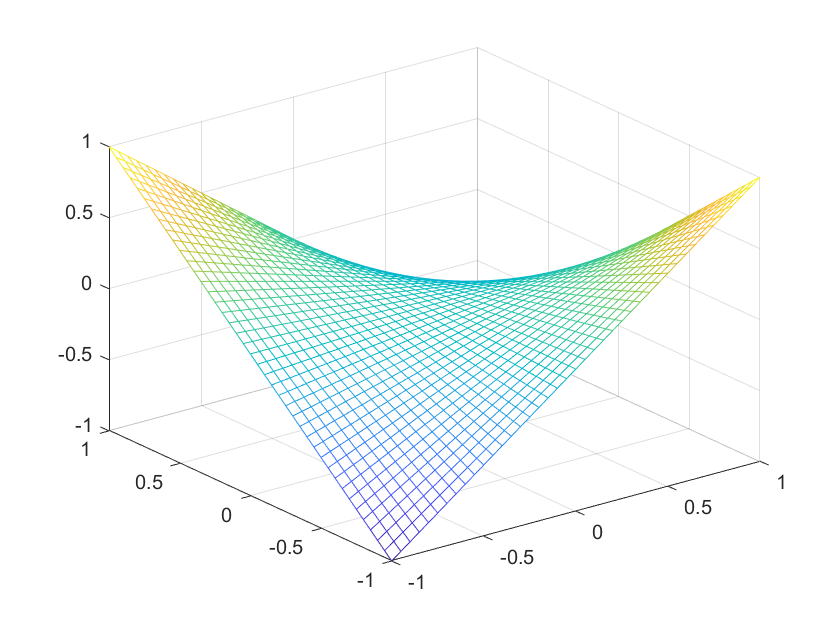
假设如下约束优化函数和约束:
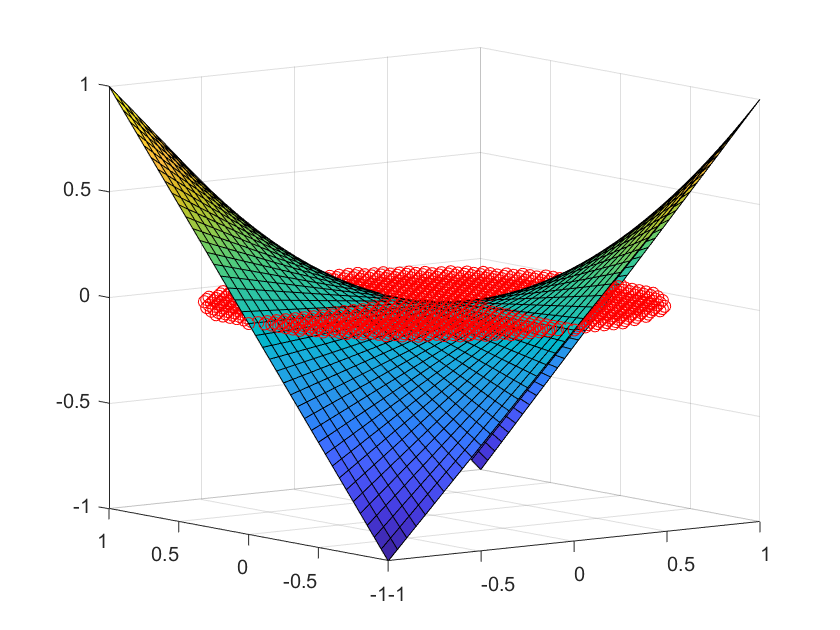
首先把这个函数的图像在Matlab中给大家画出来:
%%目标函数图像绘制
x1=-1:0.05:1;
x2=-1:0.05:1;
[x1,x2]=meshgrid(x1,x2);
y=-x1.*x2;
figure(1)
%使用mesh函数画图
mesh(x1,x2,y);
figure(2)
%使用surfl画图
% surfl(x1,x2,y);
% figure(3)
%使用surf函数画图
surf(x1,x2,y);
hold on;
%约束区域部分位置
[x1,x2]=meshgrid(-1:0.05:1);
z=1-x1.^2-x2.^2;
ind=(z>=0);
h=scatter(x1(ind),x2(ind),'r');
hold on;
%% 绘制圆柱
% 上半部分
R=1;%半径
h=-1;%圆柱高度
m=1000;%分割线的条数
[x1,y1,z1]=cylinder(R,m);%创建以(0,0)为圆心,高度为[0,1],半径为R的圆柱
z1=h*z1;%高度放大h倍
mesh(x1,y1,z1)%重新绘图
% 下半部分
hold on
R=1;%半径
h=1;%圆柱高度
m=1000;%分割线的条数
[x1,y1,z1]=cylinder(R,m);%创建以(0,0)为圆心,高度为[0,1],半径为R的圆柱
z1=h*z1;%高度放大h倍
mesh(x1,y1,z1)%重新绘图
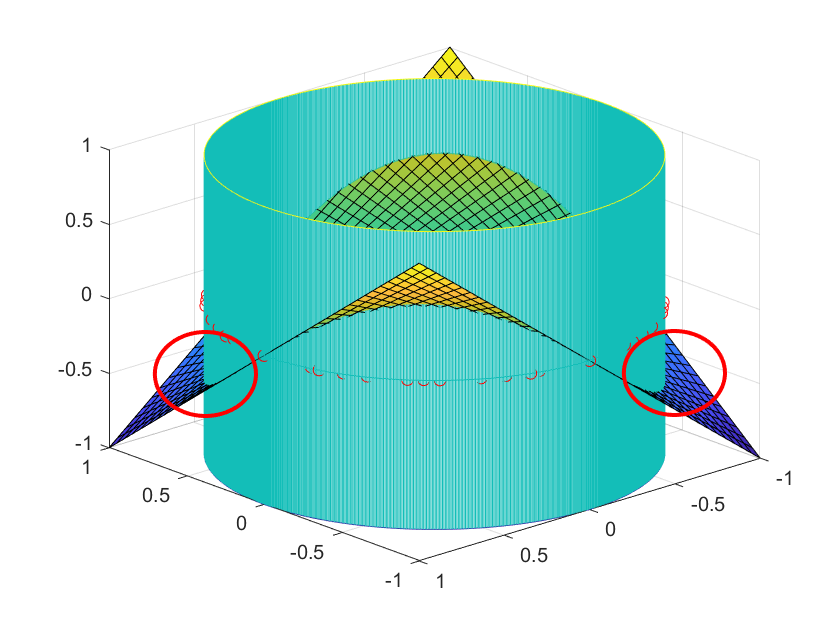
从上面第三张图中可知红色圆圈位置处有最优值,对应的最优质的大约时-0.5,下面通过优化计算查看最优值结果。
使用Matlab实现一下四种优化算法:
function [xsol, fval] = runfmincon % 初始点 x0 = [-0.1 -0.1]; % 四种优化算法,大家选一种用,这里用的是内点法 % 'active-set', 'interior-point', 'sqp', or 'trust-region-reflective'. % 在优化器中选择优化算法 options = optimset('Display', 'iter-detailed', 'Algorithm', 'interior-point', 'MaxIter', 8); % 优化器参数 % fmincon参数解释 % fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options); % fun:要优化的函数 % x0:自变量的初始值 % A:非等式(<)线性约束的约束矩阵A % b:非等式(<)线性约束的约束条件矩阵b % Aeq:等式约束的线性约束的约束矩阵Aeq % beq:等式线性约束的约束条件矩阵beq % lb,ub:自变量的下限和上限 % nonlcon:非线性约束 [xsol, fval] = fmincon(@objfun, x0, [], [], [], [], [], [], @confun, options); % 目标函数 function f = objfun(x) f = - x(1) * x(2); end % 非线性约束 function [c, ceq] = confun(x) % Nonlinear inequality constraints c = [x(1)^2 + x(2)^2 - 1]; % Nonlinear equality constraints ceq = []; end end
%在Matlab命令行窗口输入 [xsol,fval] = runfmincon; % xsol中是最优点 fval为最优点对应的最优值 % 迭代优化结果 [x1,x2]=[-0.7071,-0.7071] f=-0.5
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/30211.html