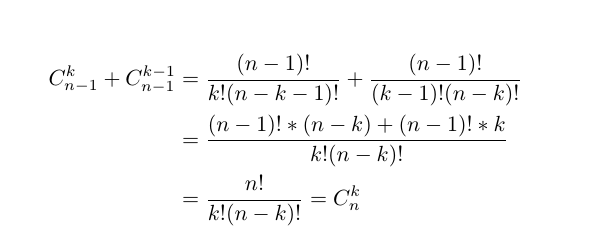组合数计算

大家好，欢迎来到IT知识分享网。

组合数的计算有好多方法，我慢慢填坑2333

1.$C_{n}^{k}=\frac{n-k+1}{k}C_{n}^{k-1}$

Proof:

$$C_{n}^{k}=\frac{n!}{k!(n-k)!}=\frac{n-k+1}{k}*\frac{n!}{(k-1)!(n-k+1)!}=\frac{n-k+1}{k}C_{n}^{k-1}.$$

利用此结论可非常快速有效的计算一个组合数了。

下给出代码：计算$C_{n}^{k}$(实际操作可将ans换成long long型)

1 int ans=1;
2 for(int i=1;i<=k;i++) {
3     ans=ans*(n-i+1)/i;
4 }
5 printf("%d\n",ans);

 2.$C_{n}^{k}=C_{n-1}^{k}+C_{n-1}^{k-1}$

证明是非常简单的，只要把相应的组合数进行展开即可：

Proof:

也可以简单的这样想：班级里有$n$个学生，班主任现在要找$k$个人去搬书，易见总共有$C_{n}^{k}$种选人方法，而所有的方法里可以分为两种：选有班长的和不选班长的．选了班长的情况下就是从$n-1$个人中再选$k-1$个人，不选班长的情况就是从$n-1$个人中选$k$个人．两种情况方案数加起来就是结果．

下给出这种方法实现组合数的代码：

 1 typedef long long ll;
 2 const ll mod=1e9+7;
 3 ll C[1005][1005];
 4 void init()
 5 {
 6     C[0][0]=1;
 7     for(int i=1;i<=1000;i++) {
 8         for(int j=0;j<=1000;j++) {
 9             if(!j) C[i][j]=1;
10             else {
11                 C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
12             }
13         }
14     }
15 }