大家好,欢迎来到IT知识分享网。
更多MATLAB数据分析视频请点击,或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016
方差分析是英国统计学家R.A.Fisher在20世纪20年代提出的一种统计方法,它有着非常广泛的应用。在生产实践和科学研究中,经验要研究生产条件或实验条件的改变对产品的质量或产量的影响。如在农业生产中,需要考虑品种、施肥量、种植密度等因素对农作物收获量的影响;又如某产品在不同的地区、不同的时期、,采用不同的销售方式,其销售量是否有差异。在诸多影响因素中,哪些是主要的,哪些是次要的,以及主要因素处于何种状态时,才能使农作物的产量和产品的销售量达到一个较高的水平,这就是方差分析索要解决的问题。
方差分析按影响分析指标的因素(也可简单成为 自变量)个数的多少,分为单因素方差分析、双因素方差分析、三因素方差分析。。。
方差分析按分析指标(也可简单称为 因变量)的个数多少,分为一元方差分析(即ANOVOA)、多元方差分析(即,MANOVOA)..
多自变量多因变量的方差分析,可以简单称为多元方差分析,当然更精确的称为“X因素Y元方差分析”,如二因素二元方差分析。
1。单因素一元方差分析
(1) MATLAB统计工具箱中提供了anova1函数,用来作单因素一元方差分析,其调用格式如下:
<1>p=anova1(x)
根据样本观测值矩阵X进行单因素一元方差分析,检验矩阵X的各列所对应的总体是否具有相同的均值,原假设是X的各列所对应的总体具有相同的均值。输出参数p是检验的p值,对于给定的显著性水平,如果p<=显著性水平,则拒绝原假设,认为X的各列所对应的总体具有不完全相同的均值,否则接受原假设,认为X的各列所对应的总体具有相同的均值。
anova1函数还生成2个图形:标准的单因一元方差分析表和箱线图。其中方差分析表把数据之间的差异分为两部分:
一.由于列均值之间的差异引起的变差(即组间变差)
二.由于每列数据与该列数据均值之间的差异引起的变差(即组内变差)
标准的单因素一元方差分析表有6列:
第一列为方差来源,方差来源有组间、组内和总计3种
第二列为各方差来源所对应的平方和(ss)
第三列为各方差来源所对应的自由度(df)
第四列为各方差来源所对应的均方(MS),MS=ss/df
第五列为F检验统计量的观测值,它是组间均方与组内均方的比值
第六列为检验的p值,是根据F检验统计量的分布提出的。
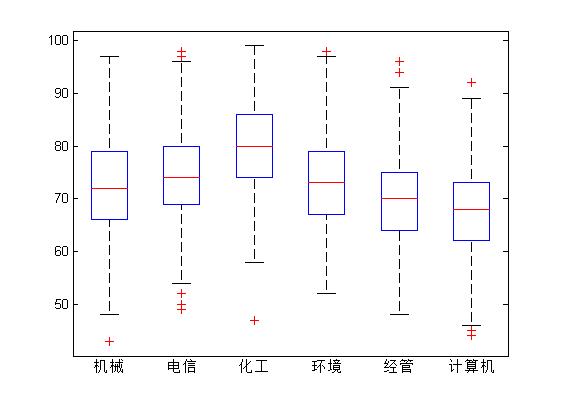
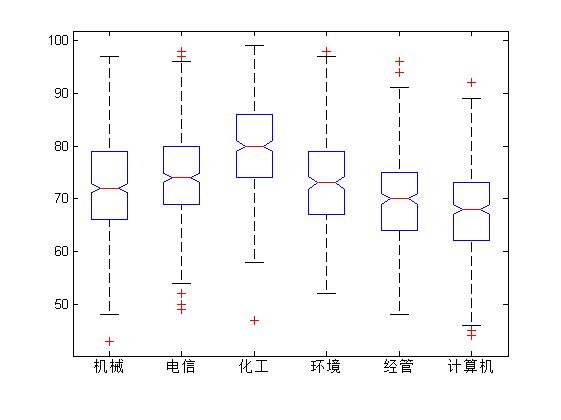
在箱线图中,X的每一列对应一个箱线图,从各个箱子中线之间的差异可以看出F检验统计量和检验的p值,较大的差异异味着较大的F值和较小的p值。
<2> p=anova1(X,group)
当X是一个矩阵时,anoval函数会把X的每一列作为一个独立的组,检验各组所对应总体是否具有相同的均值。输出参数group可以是字符串数组或字符串元胞数组,用来指定每组的组名,X的每一列对应一个组名称字符串,在箱线图中,组名字符串被作为箱线图的标签。
<3>p=anova1(X,group,displayopt)
通过displayopt参数指定是否显示方差分析表和箱线图,当displayopt参数设定为‘on‘(默认情况)时,显示方差分析表和箱线图;当displayopt参数设定为‘off’时,不显示方差分析表和箱线图。
<4>[p,table]=anova1(…..)
还返回元胞数组形式的方差分析表table(包含列标签和行标签)
<5>[p,table,stats]=anova1(….)
还返回一个结构体变量stats,用于进行后续的多重分析。anova1函数用来检验个总体是否具有相同的均值,当拒绝了原假设,认为各总体的均值不完全相同时,通常还需要进行两两的比较检验,以确定哪些总体均值间的差异是显著的,这就是所谓的多重比较。
当anova1函数给出的结果拒绝了原假设,则在后续的分析中,可以调用multcompare函数,把stats作为它的输入,进行多重比较。
样本X满足方向分析的几个基本假定:
所有样本均来自正态总体;
这些正态总体具有相同的方差。
所以在方差分析之前要做正态性检验和方差齐次性检验。
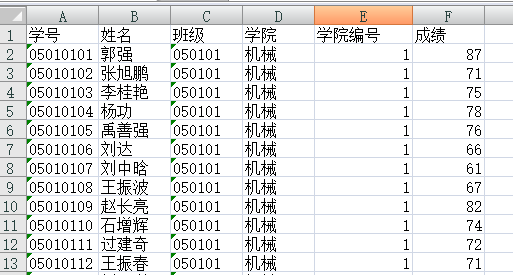
例:现有一学校的6个学院69个班级共2077名学生的数学成绩表格,现要分析不同学院的学生的成绩是否有显著性差别。
第一步:正态性检验
在调用anoval函数做方差分析之前,应先检验样本数据是否满足方差分析的基本假定,即检验正态性和方差齐次性。第一步首先做正态性检验,调用lillietest函数检验6个学院的学生的考试成绩是否服从正态分布,原假设是6个学院的学生的考试成绩服从正态分布,备择假设是不服从正态分布。
%读取文件数学成绩.xls中第一工作表中的数据
[x,y]=xlsread(‘数学成绩.xls’);
%提取矩阵x中的第2列数据,即成绩数据
score=x(:,2);
%读取元胞数组y的第4列的第2行至最后一行数据,即2077名同学所在学院名称数据
college=y(2:end,4);
%读取矩阵x的第一列数据,即2077名学生所在学院的编号数据
college_id=x(:,1);
%调用lillietest函数分布对6个学院的成绩进行正态性检验
for i=1:6
scorei=score(college_id==i); %提取第i个学院的成绩数据
[h,p]=lillietest(scorei); %正态性检验
result(i,:)=p; %把检验的p值赋给result变量
end
%检测正态检验的p值
result
result =
0.0734
0.1783
0.1588
0.1494
0.4541
0.0727
对6个学院的学生的考试成绩进行的正态检验的p值均大于0.05,说明在显著性水平0.05下均接受原假设,认为6个学院的学院的考试成绩服从正态分布。
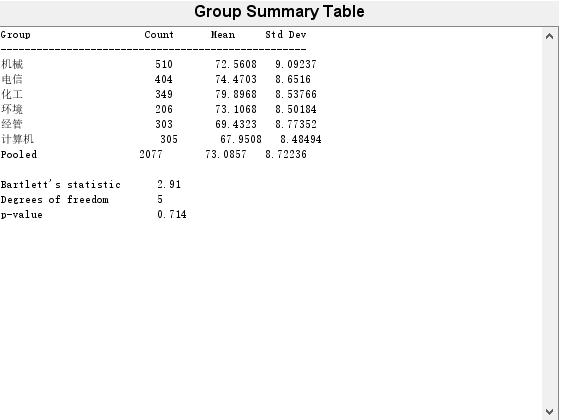
第二步:方差齐次性检验
下面调用vartestn函数检验6个学院的学生的考试成绩是否服从方差相同的正态分布,原假设是6个学院的学生的成绩服从方差相同的正态分布,备择假设是服从方差不同的正态分布。
%读取文件数学成绩.xls中第一工作表中的数据
[x,y]=xlsread(‘数学成绩.xls’);
%提取矩阵x中的第2列数据,即成绩数据
score=x(:,2);
%读取元胞数组y的第4列的第2行至最后一行数据,即2077名同学所在学院名称数据
college=y(2:end,4);
%调用vartestn函数进行方差齐次性检验
[p,stats]=vartestn(score,college)
p =
0.7138
stats =
chisqstat: 2.9104
df: 5
检验的p值=0.7138>0.05,说明在显著性水平0.05下接受原假设,认为6个学院的学生的考试成绩服从方差相同的正态分布,满足方差分析的基本假定。
第三步:方差分析
经过正态性检验和方差齐次性检验之后,认为6个学院学生的成绩服从方差相同的正态分布,下面调用anoval函数进行单因素一元方差分析,检验不同学院的学生的考试成绩有无显著差别,原假设是没有显著差别,备择假设是有显著差别。
%读取文件数学成绩.xls中第一工作表中的数据
[x,y]=xlsread(‘数学成绩.xls’);
%提取矩阵x中的第2列数据,即成绩数据
score=x(:,2);
%读取元胞数组y的第4列的第2行至最后一行数据,即2077名同学所在学院名称数据
college=y(2:end,4);
%单因素一元方差分析
[p,table,stats]=anova1(score,college)
p =
5.6876e-74
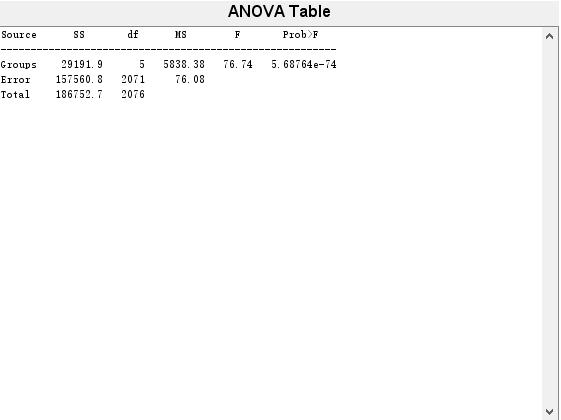
table =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘F’ ‘Prob>F’
‘Groups’ [2.9192e+04] [ 5] [5.8384e+03] [76.7405] [5.6876e-74]
‘Error’ [1.5756e+05] [2071] [ 76.0796] [] []
‘Total’ [1.8675e+05] [2076] [] [] []
stats =
gnames: {6×1 cell}
n: [510 404 349 206 303 305]
source: ‘anova1’
means: [72.5608 74.4703 79.8968 73.1068 69.4323 67.9508]
df: 2071
s: 8.7224
anova1函数返回的p值<0.05,故拒绝原假设,认为不同学院的学生的考试成绩有非常显著的差别,同时还返回的table是一个标准的单因素一元方差分析表,它的各列依次是方差来源,平方和、自由度、均方、、F值和p值。还生成了箱线图。
虽然不同学院的学生的成绩有非常显著的差别,但这并不意味着任意两个学院学生的成绩都有显著性差别,因此还需要进行两两的比较检验,即多重比较,找出考试成绩存在显著性差别的学院。
第五步:多重比较
方差分析的结果已经表明不同学院的学生的考试成绩有非常显著的差别,但这并不意味着任意两个学院学生的成绩都有显著性差别,因此还需要进行两两的比较检验,即多重比较,找出考试成绩存在显著性差别的学院。
MATLAB统计工具箱中提供了multcompare函数,用来做多重检验,其调用格式如下:
<1>c=multcompare(stats)
根据结构体变量stats中的信息进行多重比较,返回两两比较的结果矩阵c。c是一个多行5列的矩阵,它的每一行对应一次两两比较的检验,每一行上的元素包括包括作比较的两个组的组标好,两个组的均值差、均值差的置信区间。比如
2.0000 5.0000 1.9442 8.0625 14.4971
表示第2组合第5组进行两两比较,两组的均值差(第2组减去第5组的均值)为8.0625,均值差的95%的置信区间为[1.9442,14.4971],这个区间不包括0,说明在显著性水平0.05下,两组间均值的差异是显著的。
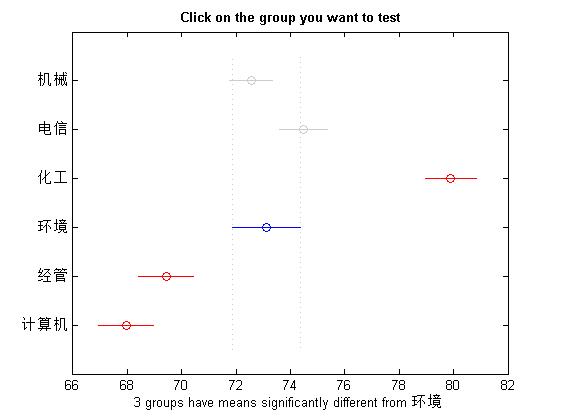
multcompare函数还生成一个交互式图形,可以通过鼠标单击的方式进行两两比较检验。该交互式图形上用一个符号(圆圈)标出了每一组的组均值,用一条之间段标出了每个组的组均值的置信区间。如果某两条线段不相交,即没有重叠的部分,则说明这两个组的组均值之间的差异是显著的。如果某两条直线段有重叠部分,则说明这两个组的组均值之间的差异是不显著的。可以用鼠标在图上任意选一个组,选中的组以及与选中的组禅意显著的其他组均用高亮显示,选中的组用蓝色显示,与选中的组差异显著的其他组用红色显示。
<2>c=multcompare(stats,param1,val1,param2,val2,…….)
指定一个或多个成对出现的参数名与参数值来控制多重比较,可用的参数值和参数名如下表:
|
参数名 |
参数值 |
说明 |
|
‘alpha’ |
(0,1)内的标量 |
用来指定输出矩阵c中的置信区间和交互式图形上的置信水平,默认值0.05 |
|
‘display’ |
‘on’ ‘off’ |
用来指定是否显示交互式图形,若为‘on’(默认情况),则显示图形;若为‘off’则不显示图形 |
|
‘ctype’ |
‘hsd’或‘tukeyk-kramer’; ‘lsd’;’bonferroni’; ‘dumn-sidak’;’scheffe’ |
指定多重比较的方法。可用的方法有Tukey-Kramer法(默认情况)、最小显著差法(LSD法)、Bonferron t检验法、Dunn-Sidak法和Scheffe法 |
|
‘dimension’ |
正整数向量 |
对于多因素方差分析的比较检验,用来指定要比较的因素(分组变量)的序号,默认值为1,表示第1个分组变量。仅适用于stats是anovan函数的输出的情形 |
|
‘estimate’ |
依赖于生成结构体变量stats所用的函数 |
指定要比较的估计,其可能取值依赖于生成的结构体变量stats所用的函数。对于anova1,anovan(多因素方差分析)、friedman(Frideman秩方差分析)和kruskalwallis(Kruskal-Wallis单因素方差分析)函数,才参数被忽略;对于anova2(双因素方差分析)函数.’estimate’参数的可能取值为‘column’(默认)或‘row’,表示对列均值或行均值进行比较;对于aoctool(交互式协方差分析)函数,‘estimate’参数的可能取值为‘slope’,‘intercept’或‘pmm’,分别表示对斜率、截距或总体边缘均值进行比较。 |
<3>[c,m]=multcompare(……)
返回一个多行2列的矩阵m,第1列为每一组均值的估计值,第2列为相应的标准误差。
<4>[c,m,b]=multcompare(…..)
返回交互式多重比较的图形的句柄值h,可通过h修改图形属性,如图形标题和X轴标签等。
<5>[c,m,b,gnames]=multcompare(……)
返回组名变量gnames,它是一个元胞数组,每一行对应一个组名。
%读取文件数学成绩.xls中第一工作表中的数据
[x,y]=xlsread(‘数学成绩.xls’);
%提取矩阵x中的第2列数据,即成绩数据
score=x(:,2);
%读取元胞数组y的第4列的第2行至最后一行数据,即2077名同学所在学院名称数据
college=y(2:end,4);
%单因素一元方差分析
[p,table,stats]=anova1(score,college)
%调用multcompare函数多重比较
[c,m,h,gnames]=multcompare(stats);
%设置表头,以元胞数组形式显示矩阵c
head={‘组序号’,’组序号’,’置信下限’,’置信上限’,’组均值差’,’置信上限’};
[head;num2cell(c)] %将矩阵c转为元胞数组,并与head一起显示
[gnames num2cell(m)] %将m转为元胞数组,和gnames一起显示
ans =
‘组序号’ ‘组序号’ ‘置信下限’ ‘置信上限’ ‘组均值差’ ‘置信上限’
[ 1] [ 2] [-3.5650] [-1.9095] [-0.2540] [ 0.0130]
[ 1] [ 3] [-9.0628] [-7.3361] [-5.6093] [2.0676e-08]
[ 1] [ 4] [-2.5980] [-0.5460] [ 1.5060] [ 0.9743]
[ 1] [ 5] [ 1.3255] [ 3.1284] [ 4.9313] [1.1298e-05]
[ 1] [ 6] [ 2.8108] [ 4.6100] [ 6.4092] [2.0679e-08]
[ 2] [ 3] [-7.2430] [-5.4266] [-3.6101] [2.0676e-08]
[ 2] [ 4] [-0.7645] [ 1.3635] [ 3.4915] [ 0.4489]
[ 2] [ 5] [ 3.1490] [ 5.0380] [ 6.9270] [2.0676e-08]
[ 2] [ 6] [ 4.6340] [ 6.5195] [ 8.4049] [2.0676e-08]
[ 3] [ 4] [ 4.6061] [ 6.7901] [ 8.9740] [2.0676e-08]
[ 3] [ 5] [ 8.5128] [10.4645] [12.4163] [2.0676e-08]
[ 3] [ 6] [ 9.9977] [11.9460] [13.8943] [2.0676e-08]
[ 4] [ 5] [ 1.4299] [ 3.6745] [ 5.9190] [4.5367e-05]
[ 4] [ 6] [ 2.9144] [ 5.1560] [ 7.3976] [2.1451e-08]
[ 5] [ 6] [-0.5346] [ 1.4815] [ 3.4976] [ 0.2902]
ans =
‘机械’ [72.5608] [0.3862]
‘电信’ [74.4703] [0.4340]
‘化工’ [79.8968] [0.4669]
‘环境’ [73.1068] [0.6077]
‘经管’ [69.4323] [0.5011]
‘计算机’ [67.9508] [0.4994]
2、双因素一元方差分析
(1.)双因素一元方差分析的MATLAB实现
MATLAB统计工具箱中提供了anova2函数,用来做双因素一元方差分析,其调用格式如下:
<1>p=anova2(X,reps)
根据样本观测值矩阵X进行均衡实验的双因素一元方差分析。X的每一列对应因素A的一个水平,每行对应因素B的一个水平,X还应满足方差分析的基本假定。reps表示因素A和B下的每一个水平组合下重复实验的次数。
anova2函数检验矩阵X的各列是否具有相同的均值,即检验因素A对实验指标的影响是否显著,原假设为:
H0A:X的各列具有相同的均值(或因素A对实验指标的影响不显著)
anova2函数还检验矩阵X的各行是否具有相同的均值,即检验因素B对实验指标的影响是否显著,原假设为:
H0B:X的各行有相同的均值(或因素B对实验指标的影响不显著)
若参数reps的取值大于1(默认值为1),anova2函数还检验因素A和因素B的交互作用是否显著,原假设为:
H0AB: A和B的交互作用不显著
anova2函数返回检验的p值,若参数reps的取值等于1,则p是一个包含2个元素的行向量;若参数是reps的取值大于1,则p是一个包含3个元素的行向量,其元素粉笔是与H0A,H0B,H0AB对应的检验的p值。当检验的p值小于或等于给定的显著性水平时,应拒绝原假设。
anova2函数还生成1个图形,用来显示一个标准的双因素一元方差分析表。方差分析表把数据之间的差异分为三部分(当reps=1时)或四部分(当reps=2时):
<2>p=anova2(X,reps,displayopt)
通过displayopt参数指定是否显示带有标准双因素一元方差分析表的图形窗口,当displayopt参数设置为‘on’(默认情况)时,显示方差分析表;当displayopt参数设定为‘off’时,不显示方差分析表。
<3>[p,table]=anova(…..)
返回元胞数组形式的方差分析表table(包含列标签和行标签)。
<4>[p,table,stats]=anova2(……)
返回一个结构体变量stats,用于进行后续的多重比较。
(2)例:为了研究肥料使用量对水稻产量的影响,某研究所做了氮(因素A)、磷(因素B)两种肥料施用量的二因素试验。氮肥用量设低、中、高三个水平,分布使用N1,N2和N3表示;磷肥用量设低、高2个水平,分别用P1,P2表示。供3×2=6个处理,重复4次,随机区组设计,测得水稻产量如下表
|
处理 |
区组 |
|||
|
1 |
2 |
3 |
4 |
|
|
N1P1 |
38 |
29 |
36 |
40 |
|
N1P2 |
45 |
42 |
37 |
43 |
|
N2P1 |
58 |
46 |
52 |
51 |
|
N2P2 |
67 |
70 |
65 |
71 |
|
N3P1 |
62 |
64 |
61 |
70 |
|
N3P2 |
58 |
63 |
71 |
69 |
根据上表中的数据,不考虑区组因素,分析氮、磷两种肥料的施用量对水稻产量是否有显著性影响,并分析交互作用是否显著。取显著性水平=0.05;
注意:这里不需要进行正态性和方差性齐次性检验,因素数据少,在数据比较少的情况下正态检验的结果是不可靠的,即使不满足方差分析的假定,方差分析的结果通常也是比较稳定的。
双因素一元方差分析首先要把数据矩阵处理一下,要把矩阵装换成每一列对应因素A的一个水平,每行对应因素B的一个水平。本例中,每一列对应一个A因素(氮)水平,每一行对应一个B因素(磷)水平;反过来也可以。
|
处理 |
区组 |
|||
|
1 |
2 |
3 |
4 |
|
|
N1P1 |
38 |
29 |
36 |
40 |
|
N1P2 |
45 |
42 |
37 |
43 |
|
N2P1 |
58 |
46 |
52 |
51 |
|
N2P2 |
67 |
70 |
65 |
71 |
|
N3P1 |
62 |
64 |
61 |
70 |
|
N3P2 |
58 |
63 |
71 |
69 |
先转置为
|
N1P1 |
N1P2 |
N2P1 |
N2P2 |
N3P1 |
N3P2 |
|
38 |
45 |
58 |
67 |
62 |
58 |
|
29 |
42 |
46 |
70 |
64 |
63 |
|
36 |
37 |
52 |
65 |
61 |
71 |
|
40 |
43 |
51 |
71 |
70 |
69 |
把第2列,第4列,第6列接到第1列,第3列,第5列下面
|
N1P1 |
N2P1 |
N3P1 |
|
38 |
58 |
62 |
|
29 |
46 |
64 |
|
36 |
52 |
61 |
|
40 |
51 |
70 |
|
N1P2 |
N2P2 |
N3P2 |
|
45 |
67 |
58 |
|
42 |
70 |
63 |
|
37 |
65 |
71 |
|
43 |
71 |
69 |
提出公共项
|
|
N1 |
N2 |
N3 |
|
P1 |
38 |
58 |
62 |
|
P1 |
29 |
46 |
64 |
|
P1 |
36 |
52 |
61 |
|
P1 |
40 |
51 |
70 |
|
P2 |
45 |
67 |
58 |
|
P2 |
42 |
70 |
63 |
|
P2 |
37 |
65 |
71 |
|
P2 |
43 |
71 |
69 |
%定义一个矩阵,输入原始数据
yield=[38 29 36 40
45 42 37 43
58 46 52 51
67 70 65 71
62 64 61 70
58 63 71 69];
yield=yield’; %矩阵转置
%将数据矩阵yield转换成8行3列的矩阵,列对应因素A(氮),行对应因素B(磷)
yield=[yield(:,[1,3,5]);yield(:,[2,4,6])];
%定义元胞数组,以元胞数组形式显示转换后的数据
top={‘因素’,’N1′,’N2′,’N3′};
left={‘P1′;’P1′;’P1′;’P1′;’P2′;’P2′;’P2′;’P2’};
%显示数据
[top;left,num2cell(yield)]
%调用anova2函数作双因素方差分析,返回检验的p值向量,方差分析表,结构体标量stats
[p,table,stats]=anova2(yield,4)
ans =
‘因素’ ‘N1’ ‘N2’ ‘N3’
‘P1’ [38] [58] [62]
‘P1’ [29] [46] [64]
‘P1’ [36] [52] [61]
‘P1’ [40] [51] [70]
‘P2’ [45] [67] [58]
‘P2’ [42] [70] [63]
‘P2’ [37] [65] [71]
‘P2’ [43] [71] [69]
p =
0.0000 0.0004 0.0080
table =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘F’ ‘Prob>F’
‘Columns’ [ 3067] [ 2] [1.5335e+03] [78.3064] [1.3145e-09]
‘Rows’ [368.1667] [ 1] [ 368.1667] [18.8000] [3.9813e-04]
‘Interaction’ [250.3333] [ 2] [ 125.1667] [ 6.3915] [ 0.0080]
‘Error’ [352.5000] [18] [ 19.5833] [] []
‘Total’ [ 4038] [23] [] [] []
stats =
source: ‘anova2’
sigmasq: 19.5833
colmeans: [38.7500 60 64.7500]
coln: 8
rowmeans: [50.5833 58.4167]
rown: 12
inter: 1
pval: 0.0080
df: 18
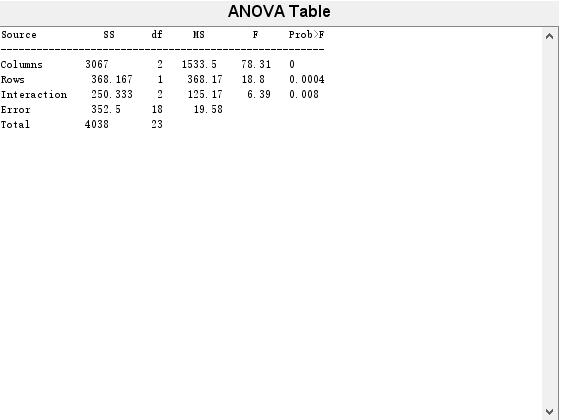
因素A、因素B以及他们的交互作用对应的检验p值均小于给定的显著性水平0.05,所以可以认为氮、磷两种肥料的施用量对水稻的产量均有显著性影响,并且他们之间的交互作用也是非常显著的。由于氮、磷两种肥料的用量对水稻的产量均有非常显著的影响,可以作进一步分析,例如进行多重分析,找出因素A、B在哪种水平的组合下水稻的平均产量最高。
(3)多重比较
下面调用multcompare函数,把anova2函数返回的结构体变量stats作为它的输入,进行多重比较。
%对列(因素A)进行多重比较
[c_A,m_A]=multcompare(stats,’estimate’,’column’)
%对行(因素B)进行多重比较
[c_B,m_B]=multcompare(stats,’estimate’,’row’)
Note: Your model includes an interaction term that is significant at the level
you specified. Testing main effects under these conditions is questionable.
c_A =
1.0000 2.0000 -26.8971 -21.2500 -15.6029 0.0000
1.0000 3.0000 -31.6471 -26.0000 -20.3529 0.0000
2.0000 3.0000 -10.3971 -4.7500 0.8971 0.1084
m_A =
38.7500 1.5646
60.0000 1.5646
64.7500 1.5646
Note: Your model includes an interaction term that is significant at the level
you specified. Testing main effects under these conditions is questionable.
c_B =
1.0000 2.0000 -11.6289 -7.8333 -4.0378 0.0004
m_B =
50.5833 1.2775
58.4167 1.2775
由上面结果可以看出,若单独考虑A因素,它的第1个水平与后两个水平差异显著,它的第2个水平与第3个水平差异不显著,并且当A去第3个水平(N3)时,水稻产量的均值达到最大(64.75);如果单独考虑B因素,它的两个水平差异显著,在因素A,B的水平组合N3P2下,水稻的平均产量达到最大值,然而这确实错误的,因为A,B之间存在着非常显著的交互作用,在这种情况下对主效应进行检验可能存在问题,这时应该对因素A、B的每种水平组合进行多重比较,找出所要的水平组合。这就是下一节的内容。
3.多因素一元方差分析
(1)多因素一元方差分析的MATLAB实现
MATLAB工具工具箱中提供了anovan函数,用来根据样本观测值向量进行均衡或非均衡试验的多因素一元方差分析,检验多个(N个)因素的主效应或交互式效应是否显著,调用格式如下:
<1>p=anovan(y,group)
根据样本观测值向量y进行均衡或非均衡试验的多因素一元方差分析,检验多个因素的主效应是否显著。输入参数group是一个元胞数组,它的每一个元胞对应一个因素,是该因素的水平列表,与y等长,用来标记y中的每个观测所对应的因素的水平。
anovan函数还生成1个图形,用来显示一个标准的多因素一元方差分析表。
<2>p=anovan(y,group,param1,val1,param2,val2,……)
通过指定一个或多个成对出现的参数名与参数值来控制多因素一元方差分析。可用的参数名与参数值如下表
|
参数名 |
参数值 |
说明 |
|
‘alpha’ |
(0,1)内的标量 |
指定置信水平 |
|
‘continuous’ |
下标向量 |
用来指明哪些分组变量被作为连续变量,而不是离散的分类变量 |
|
‘display’ |
‘on’ ‘off’ |
用来指定是否显示方差分析表 |
|
‘model’ |
‘linear’,‘interaction’ ‘full’ |
用来指定所用模型的类型,‘linear’(默认)只对N个主效应进行检验,不考虑交互效应,‘interaction’对主效应和两个因素的交互效应减小检验 ‘full’对N个主效应和全部的交互效应进行检验。 也可以通过0和1的矩阵自定义效应项 |
|
‘nested’ |
由0和1构成的矩阵M |
指定分组变量之间的嵌套关系 |
|
‘random’ |
下标向量 |
用来指明哪些分组变量是随机的。 |
|
‘sstype’ |
1,2或3 |
指定平方和的类型,默认值为3 |
|
‘varnames’ |
字符矩阵或字符串元胞数组 |
指定分组变量的名称。当没有指定时,默认用‘X1’,‘X2’,…’XN’做为名称 |
<3>[p,table]=anovan(……)
返回元胞数组形式的方差分析表table。
<4>[p,table,stats]=anovan(…..)
返回一个结构体变量stats,用于进行后续的多重比较,。当某因素对实验指标的影响显著时,在后续的分析中,可用调用multcompare函数,把stats作为其输入,进行多重比较。
<5>[p,table,stats,terms]=anovan(…..)
返回方差分析计算中的主效应和交互效应矩阵terms。
(2)例:仍用上节中的数据
|
处理 |
区组 |
|||
|
1 |
2 |
3 |
4 |
|
|
N1P1 |
38 |
29 |
36 |
40 |
|
N1P2 |
45 |
42 |
37 |
43 |
|
N2P1 |
58 |
46 |
52 |
51 |
|
N2P2 |
67 |
70 |
65 |
71 |
|
N3P1 |
62 |
64 |
61 |
70 |
|
N3P2 |
58 |
63 |
71 |
69 |
调用anovan函数进行分析,在不考虑区组因素的情况下,分析氮、磷两种肥料的施用量对水稻的产量是否有显著影响,并分析交互作用是否显著,然后找出在因素A,B的哪种水平组合下水稻的平均产量高,显著性水平为0.05.
%定义一个矩阵,输入原始数据
yield=[38 29 36 40
45 42 37 43
58 46 52 51
67 70 65 71
62 64 61 70
58 63 71 69];
yield=yield’ %矩阵转置
%将数据矩阵yield按列拉长成24行1列的向量
yield=yield(:);
%定义因素A(氮)的水平列表向量
A=strcat({‘N’},num2str([ones(8,1);2*ones(8,1);3*ones(8,1)]));
%定义因素B(磷)的水平列表向量
B=strcat({‘P’},num2str([ones(4,1);2*ones(4,1)]));
B=[B;B;B];
%将因素A、B的水平列表向量与yield向量放在一起构成一个元胞数组,以元胞数组形式显示出来
[A,B,num2cell(yield)]
%指定因素名称,A表示氮肥施用量,B表示磷肥施用量
varnames={‘A’,’B’};
%调用anovan函数作双因素一元方差分析,返回主效应A、B和交互效应AB所对应的p值向量
%还返回方差分析表table,结构体变量stats,标识模型效应项的矩阵term
[p,table,stats,term]=anovan(yield,{A,B},’model’,’full’,’varnames’,varnames)
ans =
‘N1’ ‘P1’ [38]
‘N1’ ‘P1’ [29]
‘N1’ ‘P1’ [36]
‘N1’ ‘P1’ [40]
‘N1’ ‘P2’ [45]
‘N1’ ‘P2’ [42]
‘N1’ ‘P2’ [37]
‘N1’ ‘P2’ [43]
‘N2’ ‘P1’ [58]
‘N2’ ‘P1’ [46]
‘N2’ ‘P1’ [52]
‘N2’ ‘P1’ [51]
‘N2’ ‘P2’ [67]
‘N2’ ‘P2’ [70]
‘N2’ ‘P2’ [65]
‘N2’ ‘P2’ [71]
‘N3’ ‘P1’ [62]
‘N3’ ‘P1’ [64]
‘N3’ ‘P1’ [61]
‘N3’ ‘P1’ [70]
‘N3’ ‘P2’ [58]
‘N3’ ‘P2’ [63]
‘N3’ ‘P2’ [71]
‘N3’ ‘P2’ [69]
p =
0.0000
0.0004
0.0080
table =
‘Source’ ‘Sum Sq.’ ‘d.f.’ ‘Singular?’ ‘Mean Sq.’ ‘F’ ‘Prob>F’
‘A’ [3.0670e+03] [ 2] [ 0] [1.5335e+03] [78.3064] [1.3145e-09]
‘B’ [ 368.1667] [ 1] [ 0] [ 368.1667] [18.8000] [3.9813e-04]
‘A*B’ [ 250.3333] [ 2] [ 0] [ 125.1667] [ 6.3915] [ 0.0080]
‘Error’ [ 352.5000] [ 18] [ 0] [ 19.5833] [] []
‘Total’ [ 4038] [ 23] [ 0] [] [] []
stats =
source: ‘anovan’
resid: [24×1 double]
coeffs: [12×1 double]
Rtr: [6×6 double]
rowbasis: [6×12 double]
dfe: 18
mse: 19.5833
nullproject: [12×6 double]
terms: [3×2 double]
nlevels: [2×1 double]
continuous: [0 0]
vmeans: [2×1 double]
termcols: [4×1 double]
coeffnames: {12×1 cell}
vars: [12×2 double]
varnames: {2×1 cell}
grpnames: {2×1 cell}
vnested: []
ems: []
denom: []
dfdenom: []
msdenom: []
varest: []
varci: []
txtdenom: []
txtems: []
rtnames: []
term =
1 0
0 1
1 1
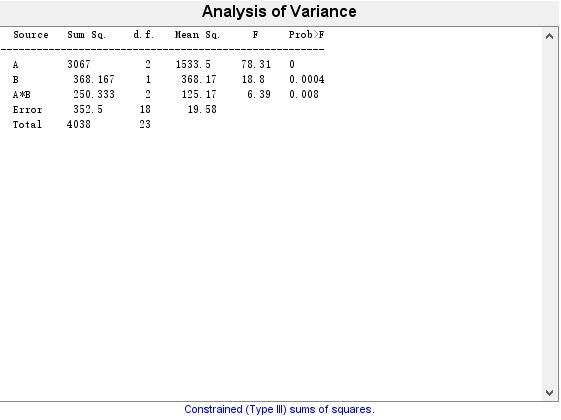
返回的向量p是主效应A,B和交互效应AB所对应的检验的p值,table是元胞数组的方差分析表,stats是一个结构体变量,可用于后续的分析中(如多重比较),矩阵term的3行分布表示了3个效应项:主效应项A,主效应项B和交互式效应项AB,还生成了一个方差分析表。
返回的结果与调用anova2函数得到的结果一样,因素A,因素B以及他们的交互作用所对应的p值均小于给定的显著想水平0.05,所以可以认为氮、磷两种肥料的施用量对水稻的产量均有非常显著的影响,并且他们之间的交互作用也是非常显著的。
(3)多重比较。
调用multcompare函数,把anovan函数返回的结构体变量stats作为它的输入,对因素A、B的每种水平的组合进行多重比较,找出在因素A、B的哪种水平组合下水稻的平均产量最高。
%多重比较
[c,m,h,gnames]=multcompare(stats,’dimension’,[1 2])
%查看各处理的均值
[gnames,num2cell(m)]
c =
1.0000 2.0000 -25.9446 -16.0000 -6.0554 0.0009
1.0000 3.0000 -38.4446 -28.5000 -18.5554 0.0000
1.0000 4.0000 -15.9446 -6.0000 3.9446 0.4236
1.0000 5.0000 -42.4446 -32.5000 -22.5554 0.0000
1.0000 6.0000 -39.4446 -29.5000 -19.5554 0.0000
2.0000 3.0000 -22.4446 -12.5000 -2.5554 0.0093
2.0000 4.0000 0.0554 10.0000 19.9446 0.0483
2.0000 5.0000 -26.4446 -16.5000 -6.5554 0.0006
2.0000 6.0000 -23.4446 -13.5000 -3.5554 0.0047
3.0000 4.0000 12.5554 22.5000 32.4446 0.0000
3.0000 5.0000 -13.9446 -4.0000 5.9446 0.7926
3.0000 6.0000 -10.9446 -1.0000 8.9446 0.9995
4.0000 5.0000 -36.4446 -26.5000 -16.5554 0.0000
4.0000 6.0000 -33.4446 -23.5000 -13.5554 0.0000
5.0000 6.0000 -6.9446 3.0000 12.9446 0.9251
m =
35.7500 2.2127
51.7500 2.2127
64.2500 2.2127
41.7500 2.2127
68.2500 2.2127
65.2500 2.2127
h =
2
gnames =
‘A=N1,B=P1’
‘A=N2,B=P1’
‘A=N3,B=P1’
‘A=N1,B=P2’
‘A=N2,B=P2’
‘A=N3,B=P2’
ans =
‘A=N1,B=P1’ [35.7500] [2.2127]
‘A=N2,B=P1’ [51.7500] [2.2127]
‘A=N3,B=P1’ [64.2500] [2.2127]
‘A=N1,B=P2’ [41.7500] [2.2127]
‘A=N2,B=P2’ [68.2500] [2.2127]
‘A=N3,B=P2’ [65.2500] [2.2127]
返回的矩阵c是6种处理(N1P1,N2P1,N3P1,N1P2,N2P2,N3P2)间多重比较的结果矩阵,每一行的前两列是进行比较的两个处理的编号,第4列是两个处理的均值之差,第3列是两个处理均值差的95%置信下限,第5列是两个处理均值差的95%置信下限,当两个处理均值差的95%置信区间不包含0时,说明在显著性水平0.05下,这两个处理均值间差异是显著的。m矩阵列出了6种处理的平均值,很明显第5个处理(即N2P2)的平均值最大,由矩阵c或交互式多重比较的图中可以得到,处理5与处理3,6差异不显著,所以可以认为第3个和第6个处理也是可以的,所以,综上,可以在处理3,5,6中做出选择,即N3P1,N2P2,N3P2。
4. 单因素多元方差分析
(1)单因素多元方差分析的MATLAB实现
MATLAB统计工具箱中提供了manoval函数,用来做单因素多元方差分析,检验多个多元正态总体是否具有相同的均值向量。调用格式如下:
<1>d=manova1(X,group)
根据样本观测值矩阵X进行单因素多元方差分析,比较X中的各组观测是否具有相同的均值向量,原假设是各组的组均值是相同的多元向量。样本观测值矩阵X是一个mxn的矩阵,它的每一列对应一个变量,每一行对应一个观测,每一个观测都是n元的。输入参数group是一个分组变量,用来标示X中的每个观测所在的组,group可以是一个分类变量、向量、字符串数组或字符串元胞数组,group的长度应该与X的行数相等,group中相同元素对应的X中的观测来自同一个总体(组)的样本。
各组的均值向量生成了一个向量空间,输出参数d是这个空间维数的估计,当d=0时,接受原假设,当d=1时在显著性水平0.05下,拒绝原假设,认为各组的组均值不全相同,但是不能拒绝他们贡献的假设;当d=2时,拒绝原假设,此时各组的组均值可能共面,但是不共线。
<2>d=manova1(X,group,alpha)
指定检验的显著性水平。返回的d是满足p>alpha的最小维数,其中p是检验的p值,此时检验各组的均值向量是否位于一个d维空间。
<3>[d,p]=manova1(……)
还返回检验的p值向量,它的第i个元素对应的原假设是:各组的均值向量位于一个i-1维空间,若p的第i个元素小于或等于给定的显著性水平,则拒绝这样的原假设。
<4>[d,p,stats]=manova1(……)
还返回一个结构体变量stats。
(2)例:
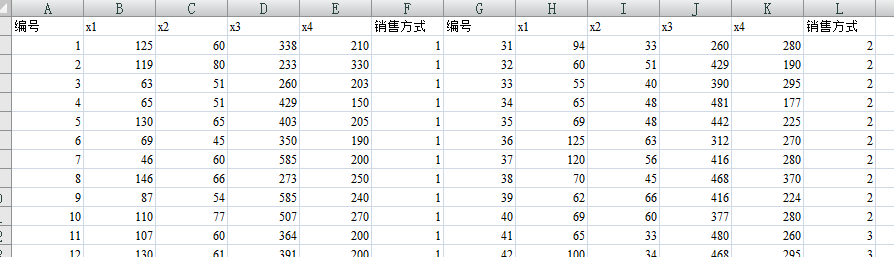
为了研究销售方式对商品的销售额的影响,选择四种商品(甲,乙,丙和丁)按三种不同的销售方式(1,2,和3)进行销售。这四种商品的销售额分别记为x1,x2,x3,x4,其数据如下表
根据这些数据分析不同销售方式对销售额是否有显著影响,显著性水平为0.05.
下面调用manova1函数作单因素多元方差分析。
%从文件销售.xls中读取数据
xdata=xlsread(‘销售.xls’);
%提取xdata的第2-5列和第8-11列,即四种商品的销售额数据
x=[xdata(:,2:5);xdata(:,8:11)];
%提取xdata的列6列和第12列,即销售方式数据
group=[xdata(:,6);xdata(:,12)];
%调用manova1函数作多元方差分析
[d,p,stats]=manova1(x,group)
d =
1
p =
0.0040
0.0917
stats =
W: [4×4 double]
B: [4×4 double]
T: [4×4 double]
dfW: 57
dfB: 2
dfT: 59
lambda: [2×1 double]
chisq: [2×1 double]
chisqdf: [2×1 double]
eigenval: [4×1 double]
eigenvec: [4×4 double]
canon: [60×4 double]
mdist: [60×1 double]
gmdist: [3×3 double]
gnames: {3×1 cell}
从manova1函数返回的结果来看,p值分别为0.004<0.05和0.0917>0.05,说明在显著性水平0.05下拒绝假设:3种销售方式所对应的销量的均值向量都相同,接受假设:3种销售方式多对应的销售量的均值向量位于一个1维空间(即共线),因此维数的估计值为d=1。总的来说,在显著性水平0.05下,可认为不同销售方式对销售额有显著影响,但是究竟对四种商品中的哪种商品的销售额影响最显著,还需要对四种商品的销售额分别做一元方差分析。
%调用anova1函数对甲商品的销售额作一元方差分析
[p1,table]=anova1(x(:,1),group)
%调用anova1函数对乙商品的销售额作一元方差分析
[p2,table2]=anova1(x(:,2),group)
%调用anova1函数对丙商品的销售额作一元方差分析
[p3,table3]=anova1(x(:,3),group)
%调用anova1函数对丁商品的销售额作一元方差分析
[p4,table4]=anova1(x(:,4),group)
p1 =
0.0411
table =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘F’ ‘Prob>F’
‘Groups’ [5.2213e+03] [ 2] [2.6106e+03] [3.3766] [0.0411]
‘Error’ [4.4070e+04] [57] [ 773.1500] [] []
‘Total’ [4.9291e+04] [59] [] [] []
p2 =
0.2078
table2 =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘F’ ‘Prob>F’
‘Groups’ [ 518.5333] [ 2] [259.2667] [1.6154] [0.2078]
‘Error’ [9.1481e+03] [57] [160.4921] [] []
‘Total’ [9.6666e+03] [59] [] [] []
p3 =
0.8478
table3 =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘F’ ‘Prob>F’
‘Groups’ [2.4808e+03] [ 2] [1.2404e+03] [0.1656] [0.8478]
‘Error’ [4.2703e+05] [57] [7.4917e+03] [] []
‘Total’ [4.2951e+05] [59] [] [] []
p4 =
8.6070e-04
table4 =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘F’ ‘Prob>F’
‘Groups’ [3.8529e+04] [ 2] [1.9265e+04] [8.0085] [8.6070e-04]
‘Error’ [1.3712e+05] [57] [2.4055e+03] [] []
‘Total’ [1.7564e+05] [59] [] [] []
对四种商品的销售额分别做了一元方差分析,得到的检验p值分别为:p1<0.05, p2>0.05,p3>0.05,p4<0.05,所以在显著性水平0.05下,可认为不同销售方式对甲商品的销售额有显著影响,对丁商品的销售额有十分显著的影响,对乙和丙商品的销售额没有显著影响。
5.非参数方差分析
前面介绍的方差分析均要求样本总体来自正态分布,并且这些正态总体应具有相同的方差,在这样的基本假定(正态性假定和方差齐次性假定)下检验总体均值是否相等,这属于参数检验。当数据不满足正态性和方差齐次性假定时,参数检验可能会出现错误,此时应该采用基于秩的非参数检验,这里介绍的是Kruskal-Wallis(KW)检验和Friedman检验
一:非参数Kruskal-Wallis(KW)检验
(1)Kruskal-Wallis(KW)检验的MATLAB实现
MATLAB统计工具箱中提供了kruskalwallis函数,用来做Kruskal-Wallis检验(单因素非参数方差分析),检验的原假设是:k个独立样本来自于相同的总体。调用格式如下:
<1>p=kruskalwallis(X)
根据样本观测值矩阵X进行Kruskal-Wallis检验,检验矩阵X的各列是否来自于相同的总体,X是一个mxn的矩阵,X的每一列是一个独立的样本,包含m个相互独立的观测。返回检验的p值,如果p小于等于显著性水平,拒绝原假设,否则接受原假设,原假设表示X的各列来自于相同的总体。
<2>p=kruskalwallis(X,group)
当X是一个矩阵时,用group参数(一个字符数组或字符串元胞数组)设定箱线图的标签,group的每一行(或每个元胞)与X的每一列对应,也就是说group的长度等于X的列数。 如果X是一个向量,此时用group来指定X的每个元素(观测值)所在的组。
<3>p=kruskalwallis(X,group,displayopt)
通过displayopt参数设定是否显示方差分析表和箱线图,当displayopt参数设定为‘on’时(默认)显示方差分析表和箱线图;设为‘off’时,不显示方差分析表和箱线图。
<4>[p,table,stats]=krusalwallis(……)
还返回元胞数组形式的方差分析表table。
<5>[p,table,stats]=kruskalwallis(….)
还返回一个结构体变量stats,用于后续的多重比较。当kruskalwallis函数给出的结果拒绝了原假设,则在后续的分析中,可以调用multcompare函,把stats作为它的输入参数,进行多重比较。
(2)例:某灯泡厂有四种不同配料方案制成的灯丝生产四批灯泡,每一批中随机抽取若干个做寿命试验,寿命数据如下表:
|
灯丝配料方案 |
灯泡寿命/h |
|
A1 |
1600 1610 1650 1680 1700 1720 1800 |
|
A2 |
1580 1640 1600 1650 1660 |
|
A3 |
1460 1550 1600 1620 1640 1610 1540 1620 |
|
A4 |
1510 1520 1530 1570 1600 1680 |
根据上表中的数据分析灯丝的不同配料方案对灯泡寿命有无显著影响。显著性水平为0.05
灯泡寿命通常不服从正态分布,不满足参数方差分析的基本假定,应该做非参数检验,下面调用kruskalwallis函数作非参数Kruskal-Wallis检验,调用anova1函数作参数检验,对比检验结果。检验的原假设:灯丝的不同配料方案对灯泡寿命无显著影响。
%第1种配料方案的灯泡的寿命,需要转置
A1=[1600,1610,1650,1680,1700,1720,1800]’;
%repmat函数,其功能是以第一个参数的内容堆叠在和A1同纬度的矩阵阵g1中
%是group参数的一部分,用来指定观测值所在的分组
g1=repmat({‘A1’},size(A1));
%第2种配料方案
A2=[1580,1640,1600,1650,1660]’;
g2=repmat({‘A2’},size(A2));
%第3种配料方案
A3=[1460,1550,1600,1620,1640,1610,1540,1620]’;
g3=repmat({‘A3’},size(A3));
%第4种
A4=[1510,1520,1530,1570,1600,1680]’;
g4=repmat({‘A4’},size(A4));
%将4种配料方案的灯泡寿命放在一起构成一个向量
life=[A1;A2;A3;A4];
group=[g1;g2;g3;g4];
%调用kruskalwallis函数作Kruskal-Wallis检验
[p1,table1,stats1]=kruskalwallis(life,group)
%调用anova1函数作单因素一元方差分析
[p2,table2]=anova1(life,group)
p1 =
0.0213
table1 =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘Chi-sq’ ‘Prob>Chi-sq’
‘Groups’ [564.7908] [ 3] [188.2636] [9.7043] [ 0.0213]
‘Error’ [890.2092] [22] [ 40.4641] [] []
‘Total’ [ 1455] [25] [] [] []
stats1 =
gnames: {4×1 cell}
n: [7 5 8 6]
source: ‘kruskalwallis’
meanranks: [20.1429 15.3000 10.5625 8.1667]
sumt: 90
p2 =
0.0092
table2 =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘F’ ‘Prob>F’
‘Groups’ [5.2951e+04] [ 3] [1.7650e+04] [4.9150] [0.0092]
‘Error’ [7.9003e+04] [22] [3.5911e+03] [] []
‘Total’ [1.3195e+05] [25] [] [] []
kruskalwallis函数返回的检验值p=0.0213<0.05,anova1函数返回的p值p=0.0092<0.05,说明在显著性水平0.05下,两种检验均拒绝了原假设,认为灯丝的不同配料方案对灯泡有显著影响。为了进一步分析anova1函数和kruskalwallis函数的区别,即分析参数检验和非参数检验的区别,将A1方案中的1800改为2800,其他数据不变,然后再次调用这两个函数进行单因素一元方差分析。
%第1种配料方案的灯泡的寿命,需要转置,把最后一个值由1800改为2800
A1=[1600,1610,1650,1680,1700,1720,2800]’;
%repmat函数,其功能是以第一个参数的内容堆叠在和A1同纬度的矩阵阵g1中
%是group参数的一部分,用来指定观测值所在的分组
g1=repmat({‘A1’},size(A1));
%第2种配料方案
A2=[1580,1640,1600,1650,1660]’;
g2=repmat({‘A2’},size(A2));
%第3种配料方案
A3=[1460,1550,1600,1620,1640,1610,1540,1620]’;
g3=repmat({‘A3’},size(A3));
%第4种
A4=[1510,1520,1530,1570,1600,1680]’;
g4=repmat({‘A4’},size(A4));
%将4种配料方案的灯泡寿命放在一起构成一个向量
life=[A1;A2;A3;A4];
group=[g1;g2;g3;g4];
%调用kruskalwallis函数作Kruskal-Wallis检验
[p1,table1,stats1]=kruskalwallis(life,group)
%调用anova1函数作单因素一元方差分析
[p2,table2]=anova1(life,group)
p1 =
0.0213
table1 =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘Chi-sq’ ‘Prob>Chi-sq’
‘Groups’ [564.7908] [ 3] [188.2636] [9.7043] [ 0.0213]
‘Error’ [890.2092] [22] [ 40.4641] [] []
‘Total’ [ 1455] [25] [] [] []
stats1 =
gnames: {4×1 cell}
n: [7 5 8 6]
source: ‘kruskalwallis’
meanranks: [20.1429 15.3000 10.5625 8.1667]
sumt: 90
p2 =
0.1738
table2 =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘F’ ‘Prob>F’
‘Groups’ [2.9119e+05] [ 3] [9.7064e+04] [1.8156] [0.1738]
‘Error’ [1.1761e+06] [22] [5.3461e+04] [] []
‘Total’ [1.4673e+06] [25] [] [] []
Kruskal-Wallis检验是基于秩的非参数检验,上面将样本观测数据中的最大值进一步增大,并没有改变样本的秩,所以两次调用kruskalwallis函数得到的结果是完全相同的,这说明Kruskal-Wallis检验不受个别异常值的影响。而改变一个数据后调用anova1函数得到的结果与改变前是相反的,这反映了参数检验的局限性,当样本数据不满足参数方差分析的基本假定时,最好用非参数方差比较检验。
(3)多重比较
由于Kruskal-Wallis非参数检验认为灯丝是不同配料方案对灯泡寿命有显著影响,下面通过多重比较来检验在哪种配料方案下灯泡寿命的差异是显著的。
%调用multcompare函数对不同配料方案下灯泡的寿命进行多重比较
[c,m,h,gnames]=multcompare(stats1);
[gnames,num2cell(m)] %把矩阵m转换为元胞数组,与gnames放在一起显示
c =
1.0000 2.0000 -6.6331 4.8429 16.3188 0.6993
1.0000 3.0000 -0.5630 9.5804 19.7237 0.0722
1.0000 4.0000 1.0724 11.9762 22.8800 0.0247
2.0000 3.0000 -6.4356 4.7375 15.9106 0.6961
2.0000 4.0000 -4.7344 7.1333 19.0010 0.4110
3.0000 4.0000 -8.1888 2.3958 12.9804 0.9377
ans =
‘A1’ [20.1429] [2.8835]
‘A2’ [15.3000] [3.4117]
‘A3’ [10.5625] [2.6972]
‘A4’ [ 8.1667] [3.1145]
从上面结果中可以看出,在显著性水平0.05下,灯丝的第1、4两种配料方案所对应的灯泡寿命的差异是显著的,其余配料方案所对应的灯泡寿命的差异是不显著的,并且第1种方案的平均秩最大,即灯丝的第一种配料方案所对应的灯泡的寿命最长。
二:非参数Frideman检验
(1)Frideman检验的MATLAB实现
MATLAB统计工具箱中提供了friedman函数,用来做非参数Friedman检验(双因素只方差分析)。调用格式:
<1>p=friedman(X,regs)
根据样本观测值矩阵X进行均衡实验的非参数Fiedman检验。X的每一列对应参数A的一个水平,每行对应因素B的一个水平。reps表示因素A和B的每一个水平组合下重复的实验次数,默认值为1。
friedman函数检验矩阵X的各列是否来自于相同的总体,即检验因素A的各水平之间无显著差异,他对分组因素B不感兴趣。Frideman函数返回检验的p值,当检验的p值小于或等于给定的显著性水平时,应拒绝原假设,原假设认为X总体来自于相同的总体。
frideman函数还生成1个图像,用来显示一个方差分析表。
<2>p=friedman(X,reps,displayopt)
通过参数displayopt参数设定是否显示带有标准双因素一元方差分析的图形窗口,当displayopt参数设定为‘on’时(默认情况),显示方差分析表;当displayopt参数设定为‘off’时,不显示方差分析表。
<3>[p,table]=friedman(……)
还返回元胞数组形式的方差分析表table。
<4>[p,table,stats]=friedman(……)
还返回一个结构体变量stats,用于进行后续的多重比较。当friedman函数给出的结果拒绝了原假设,则在后续的分析中,可以调用multcompare函数,把stats作为它的输入,进行多重比较。
(2)例:设有来自A、B、C、D四个地区的四名厨师制作名菜:水煮鱼,想比较他们的品质是否相同。四位美食评论对四名厨师的菜品分布做出了评分,如下表:
|
美食评委 |
地区 |
|||
|
A |
B |
C |
D |
|
|
1 |
85 |
82 |
82 |
79 |
|
2 |
87 |
75 |
86 |
82 |
|
3 |
90 |
81 |
80 |
76 |
|
4 |
80 |
75 |
81 |
75 |
根据表中的数据检验四个地区制作的水煮鱼这道菜的品质有无差别,去显著性水平为0.05
调用frideman函数作非参数Frideman检验,检验的原假设:四个地区的水煮鱼这道菜的品质没有区别。
%定义样本观测值矩阵x
x=[85 82 82 79
87 75 86 82
90 81 80 76
80 75 81 75];
%调用friedman函数作Frideman检验,返回检验的p值,方差分析表table和结构体变量stats
[p,table,stats]=friedman(x)
p =
0.0434
table =
‘Source’ ‘SS’ ‘df’ ‘MS’ ‘Chi-sq’ ‘Prob>Chi-sq’
‘Columns’ [12.8750] [ 3] [4.2917] [8.1316] [ 0.0434]
‘Error’ [ 6.1250] [ 9] [0.6806] [] []
‘Total’ [ 19] [15] [] [] []
stats =
source: ‘friedman’
n: 4
meanranks: [3.7500 2 2.8750 1.3750]
sigma: 1.2583
返回的检验p值p=0.0434<0.05,说明在显著性水平0.05下拒绝原假设,认为四个地区制作的水煮鱼的品质有显著性差别。具体是哪两个地区制作的水煮鱼这道菜的品质有显著差别,还需要作多重比较。
%调用multcompare函数对四个地区制作的水煮鱼这道菜的品质进行多重比较
[c,m]=multcompare(stats);
c %查看多重比较的结果矩阵c
[{‘A’;’B’;’C’;’D’},num2cell(m)] %把m矩阵转换为元胞数组,与组名放在一起显示
c =
1.0000 2.0000 -0.5358 1.7500 4.0358 0.2006
1.0000 3.0000 -1.4108 0.8750 3.1608 0.7589
1.0000 4.0000 0.0892 2.3750 4.6608 0.0381
2.0000 3.0000 -3.1608 -0.8750 1.4108 0.7589
2.0000 4.0000 -1.6608 0.6250 2.9108 0.8962
3.0000 4.0000 -0.7858 1.5000 3.7858 0.3311
ans =
‘A’ [3.7500] [0.6292]
‘B’ [ 2] [0.6292]
‘C’ [2.8750] [0.6292]
‘D’ [1.3750] [0.6292]
从以上结果可以看出,c矩阵的第3行的第3列和第5列构成的区间不包括0,说明在显著性水平0.05下,可认为A,D两个地区制作的水煮鱼这道菜的品质之间的差异是显著的。
更多MATLAB数据分析视频请点击,或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/11088.html