大家好，欢迎来到IT知识分享网。

1拉氏变换的性质

2复域传递函数

clear all
m=10;c=1.5;k=3;
a=-c/(2*m);
b=sqrt(k/m-c^2/(4*m^2));
lambda(1)=a+j*b;
lambda(2)=a-j*b;
[sigma,omega]=meshgrid(-0.2:0.01:-0.0,-1:0.02:1);
s=sigma+j*omega;
H=(1.0/m).*(1.0./((s-lambda(1)).*(s-lambda(2))));
%mesh(sigma,omega,real(H));
%pause
%mesh(sigma,omega,imag(H));
%pause
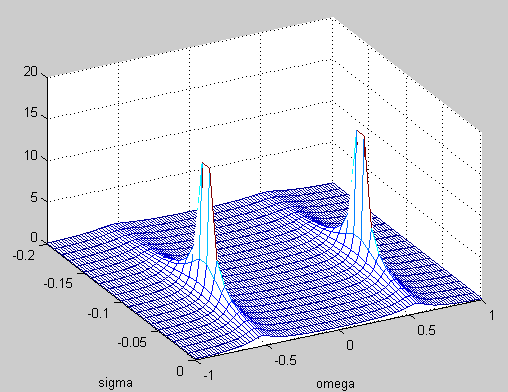
mesh(sigma,omega,abs(H));
xlabel('sigma');
ylabel('omega');

复域传递函数的自变量及因变量均是复数变量，其极点横平面坐标为特征根，可由此得到系统的自然频率、阻尼频率及阻尼比。

>> omegan=sqrt(k/m)

omegan =

    0.5477
    
 >> abs(lambda)

ans =

    0.5477    0.5477

>> zeta=c/(2*sqrt(m*k))

zeta =

    0.1369
>> -real(lambda)/omegan

ans =

    0.1369    0.1369
>> omegad=sqrt(1-zeta^2)*omegan

omegad =

    0.5426
>> lambda

lambda =

  -0.0750 + 0.5426i  -0.0750 - 0.5426i