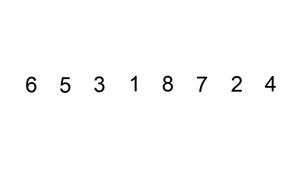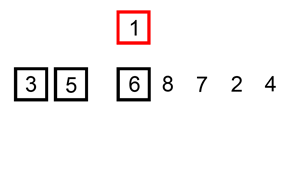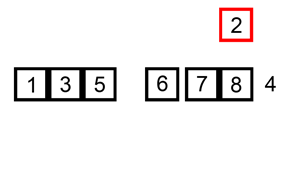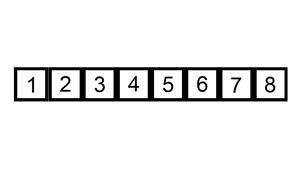大家好,欢迎来到IT知识分享网。
文章目录
三、插入排序
1、插入排序原理
每次处理就是将无序数列的第一个元素与有序数列的元素从后往前逐个进行比较,找出插入位置,将该元素插入到有序数列的合适位置中。
插入排序,顾名思义其基本操作就是插入,不断把一个个元素插入到一个序列中,最终得到排序序列。
插入排序就像打牌一样,当你摸到比较小的牌时,通常往后放,遇到比较大的牌时,通常往前方。当然了,还要看自己个人习惯。
在打牌时,我们通常每次从桌子摸一张牌,然后把这张牌再放到一个正确的位置。
为了找到这张牌放置的正确位置,我们从左到右(或者从右到左)进行比较。
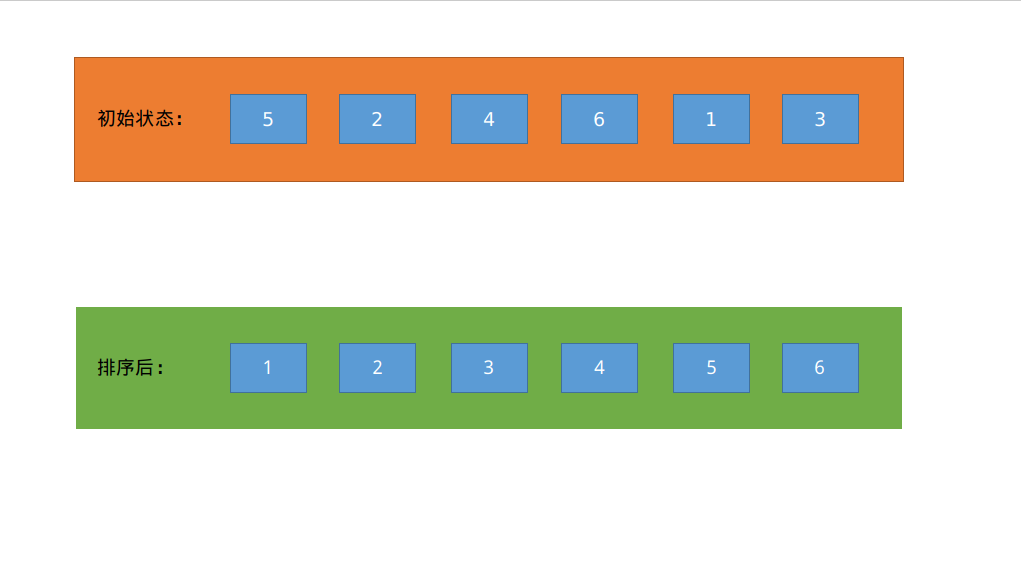
2、图解插入排序
第一轮:
i=2第二个数与前面的数做比较,发现2比5小则把小的往前方,把大的往后放
第二轮:
i+1=3第二轮时,从第三个数与前面的作比较,发现比5小,把2大,则把5往后移动
第三轮:
i+1=4第三轮时,因为是i+1,所以这次是第4个数与前面的数作比较,发现自己就是最大的,则不调整位置
第四轮:
i+1=5第四轮从第5个数开始比较,发现比2小,则放在2的前面,2和后面的都向后移动调整位置。
第五轮:
i+1=6从第6个数依次向前比较,找到2号(按照数组的索引:0,1,2)位置,则插入此位置,并把后面的依次往后移动。
完成:
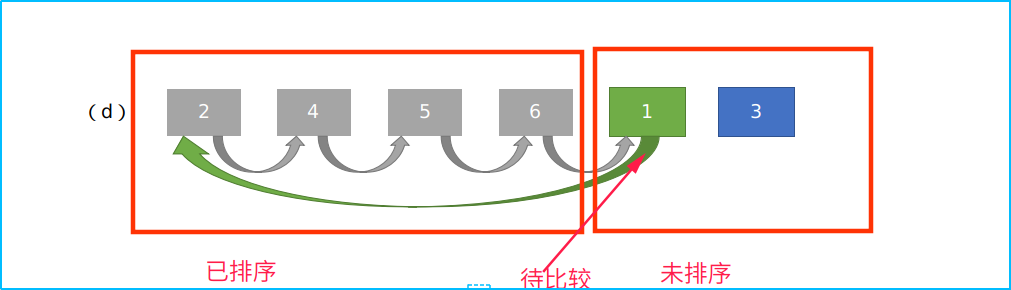
3、插入排序思路
如上图所示,此排序需要维护一个数组中的两个列表,可以把插入排序的数组分成已排序和未排序的数组。
排序的过程中只需要维护已排序的部分即可。
每次拿未排序列表的首个数与已排序的列表的数据依次作比较。
找到合适的位置后,移动这些的位置然后插入进来即可完成插入的操作。
步骤:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果被扫描的元素(已排序)大于新元素,将该元素后移一位
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
4、代码实现插入排序
从小到大:
package 排序算法.插入排序;
import java.util.Arrays;
/** * @Auther: truedei * @Date: 2020 /20-6-6 22:59 * @Description: */
public class InsertionSort {
public static int[] INSERTION_SORT(int[] ints){
//所有参与排序的数组的索引范围,为什么从1开始呢,因为可以把0号位置的数据当成已经排序好的
for (int i = 1; i < ints.length; i++) {
//一直到排到的第i个位置结束,进行倒着比较
for (int j = i; j >0 ; j--) {
//比较,如果符合要求则交换位置
if(ints[j] < ints[j-1]){
int temp = ints[j];
ints[j]=ints[j-1];
ints[j-1]=temp;
}else {
//遇到不符合要求的数据则停止,代表前面都是最小或者最大的了
break;
}
}
}
return ints;
}
public static void main(String[] args) {
System.out.println(Arrays.toString(INSERTION_SORT(new int[]{
2,5,4,7,6,1,3})));
}
}
结果:
[1, 2, 3, 5, 4, 6, 7]
从大到小:
package 排序算法.插入排序;
import java.util.Arrays;
/** * @Auther: truedei * @Date: 2020 /20-6-6 22:59 * @Description: */
public class InsertionSort {
public static int[] INSERTION_SORT(int[] ints){
//所有参与排序的数组的索引范围,为什么从1开始呢,因为可以把0号位置的数据当成已经排序好的
for (int i = 1; i < ints.length; i++) {
//一直到排到的第i个位置结束,进行倒着比较
for (int j = i; j >0 ; j--) {
//比较,如果符合要求则交换位置
if(ints[j] > ints[j-1]){
int temp = ints[j];
ints[j]=ints[j-1];
ints[j-1]=temp;
}else {
//遇到不符合要求的数据则停止,代表前面都是最小或者最大的了
break;
}
}
}
return ints;
}
public static void main(String[] args) {
System.out.println(Arrays.toString(INSERTION_SORT(new int[]{
2,5,4,7,6,1,3})));
}
}
结果:
[7, 6, 5, 4, 3, 2, 1]
[7, 6, 5, 4, 3, 2, 1]
5、时间复杂度分析
插入排序使用了双层for循环,其中内层循环体是真正完成排序的代码,所以我们分析插入排序的时间复杂度时忽略其他的,主要分析一下内层循环体的时间复杂度即可;
可以注意到该算法就两个操作是有用的:
- 一个是
比较数据 - 一个是
交换数据
最坏的情况:
比较数据次数:
最坏的情况就是从头到尾进行比较
( N − 1 ) + ( N − 2 ) + ( N − 3 ) + . . . + 2 + 1 = ( ( N − 1 ) + 1 ) × N − 1 2 = N 2 2 − N 2 (N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)×\frac {N-1}{2}=\frac{N^{2}}{2}-\frac{N}{2} (N−1)+(N−2)+(N−3)+...+2+1=((N−1)+1)×2N−1=2N2−2N
交换数据次数:
最坏的情况就是从头到尾进行交换
( N − 1 ) + ( N − 2 ) + ( N − 3 ) + . . . + 2 + 1 = ( ( N − 1 ) + 1 ) × N − 1 2 = N 2 2 − N 2 (N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)×\frac {N-1}{2}=\frac{N^{2}}{2}-\frac{N}{2} (N−1)+(N−2)+(N−3)+...+2+1=((N−1)+1)×2N−1=2N2−2N
时间复杂度就是:
( N 2 2 − N 2 ) + ( N 2 2 − N 2 ) = N 2 − N (\frac{N^{2}}{2}-\frac{N}{2})+(\frac{N^{2}}{2}-\frac{N}{2})=N^{2}-N (2N2−2N)+(2N2−2N)=N2−N
根据大O推导法则,保留最高阶项: 去掉常数项还剩下:
N 2 N^{2} N2
所以最终得出时间复杂度为:
O ( N 2 ) O(N^{2}) O(N2)
6、小技巧:常用时间复杂度
(1) O(1)
(1)O(1) 这个针对的是常数;对于一个N,不管这个N是如何增长,这个时间是不变的。
例如下面这些代码的时间复杂度都是O(1):
/** * @Auther: truedei * @Date: 2020 /20-6-2 22:01 * @Description: */
public class Test {
public static void main(String[] args) {
System.out.println("你好,我叫郑晖");
System.out.println("你好,我叫郑晖");
System.out.println("你好,我叫郑晖");
System.out.println("你好,我叫郑晖");
}
}
还有这种:
我有一个数组,我知道了我需要的这个数据所在的索引,然后去拿这个值,咋这种也是O(1)
/** * @Auther: truedei * @Date: 2020 /20-6-2 22:01 * @Description: */
public class Test {
public static void main(String[] args) {
String[] names = {
"小明","小红","郑晖"};
System.out.println("你好,我叫"+names[2]);
}
}
(2) O(n)
O(n)是一个线性增长的。
经常用在for()循环当中
例如下面这种代码:
/** * @Auther: truedei * @Date: 2020 /20-6-2 22:01 * @Description: */
public class Test {
public static void main(String[] args) {
String[] names = {
"小明","小红","郑晖"};
for (int i = 0; i < names.length; i++) {
System.out.println("你好,我叫"+names[i]);
}
}
}
(3) O(n^2)
是一个平方级的的增长。经常出现在两层for循环。
例如本文所写的:
public static int[] sort(int A[]){
for (int i = 0; i < A.length; i++) {
for (int j = 0; j < A.length -i - 1 ; j++) {
.....
}
}
return A;
}
(4) O(n^3)
是一个立方级的增长。经常出现在遍历一个三层的for循环中
for (...) {
for (...) {
for (...) {
.....
}
}
}
(5) O(lg n)
是一个对数级。
在二分查找法里就是O(lg n)。
每次执行N是以一个倍数的形式是递减的:
比如第1次:1/2
比如第2次:1/4
比如第3次:1/8
比如第4次:1/16
…
快速的让N的规模变小。
(6) O(n lg n)
在排序中经常见到的
(7) O(2^n)
指数级的
7、附:常用的排序算法的时间复杂度和空间复杂度
| 排序法 | 最差时间分析 | 平均时间复杂度 | 稳定度 | 空间复杂度 |
|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 快速排序 | O(n^2) | O(n*log2n) | 不稳定 | O(log2n)~O(n) |
| 选择排序 | O(n^2) | O(n^2) | 不稳定 | O(1) |
| 二叉树排序 | O(n^2) | O(n*log2n) | 不一顶 | O(n) |
| 插入排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 堆排序 | O(n*log2n) | O(n*log2n) | 不稳定 | O(1) |
| 希尔排序 | O | O | 不稳定 | O(1) |
如果对你有帮助,可以分享给你身边的朋友。或者给俺点个大大的赞和大大的评论,点赞和评论就是给我最大的支持,感谢。
水平有限,难免会有疏漏或者书写不合理的地方,欢迎交流讨论。
作者:TrueDei
作者唯一博客CSDN:https://truedei.blog.csdn.net/
转载说明:如需转载请注明原地址和作者名。
如果喜欢我的文章,还没看够可以关注我,我会用心写好每一篇文章。
欢迎大佬们加入在下的小社区:
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/23468.html