大家好,欢迎来到IT知识分享网。
前言
在极化码编码时,首先要区分出N个分裂信道的可靠程度,即哪些属于可靠信道,哪些属于不可靠信道。对各个极化信道的可靠性进行度量常用的有三种方法:巴氏参数(Bhattacharyya Parameter)法、密度进化(Density Evolution,DE)法和高斯近似(Gaussian Approximation)法。
目录
极化码的巴氏参数构造算法_不想秃头的男孩的博客-CSDN博客_极化码的构造方法
一 子信道评估和排序
这个方向也可以结合机器学习或者深度学习去优化.做出很多模型出来。
一方面每个子信道的可靠度通过实际测试得到相应的排序(大数定律),
然后通过回归算法,获得BP,DNN等经典算法就出每个channel的权重系数。
优点是更加灵活
定义一个(N,K)的Polar码:
将K个消息比特放在n个子信道最可靠的K个子信道上.
在子信道集合称为消息比特集合,记作 M
将剩余(N-K)个子信道放置在固定的冻结比特 记作F
Polar 的性能受到信息比特集合M的影响,确定M首先要对各个子信道
的可靠性进行评估和排序。
子信道的评估和排序主要方法有两种:
DE 密度演进, PW 权重极化, 查表
下面的理论详细推导过程,后面我在介绍LDPC 背景知识的时候会讲解一下
,例如SPC
1.1 DE(Density Evolution)密度演化
DE 的详细推导过程后面会专门介绍
这是一种跟踪概率密度在置信传输(BP Belief Propagation)
定义接收端的对数似然LLR(Log-Likelihood Ratio)
在接收端收到信息Y的时候,如果

2 PW 极化权重
这个可以结合机器学习和深度学习去优化。
这是一种直接追踪子信道经历的极化过程来评估子信道可靠度。
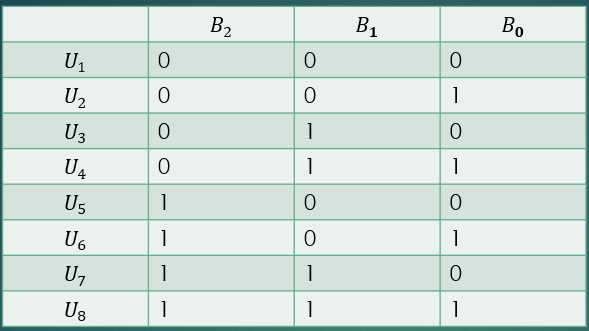
将子信道序号i用二进制表示:


则信道极化的过程与二进制序号具有一一对应的关系。
1: 对应于正向极化
0: 对应反向极化
如下为N=8
定义子信道的可靠度为

对于AWGN 信道
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 19 09:28:39 2022
@author: chengxf2
"""
import numpy as np
def getv(i,b,n):
binary = bin(i)[2:]
binary = binary[::-1] #因为从最低位开始取的
#print("\n binary ",binary)
N = len(binary)
#从最低位开始计算
v = 0.0
for j in range(n):
if j>=N:
continue
else:
a = np.power(b,j)
k = int(binary[j])
v= v+k*a
#print("\n v: ",v)
return v
'''
极化权重
'''
def pw(N=8,b=np.power(2,1/4)):
print("\n b:%f"%b)
n = np.log2(N)
for i in range(0,N):
v= getv(i,b,int(n))
print("\n i: %d"%i, "\t v :%3.2f"%v)
pw()3. 查表
TS38.212 表 5.3.1.2-1 Polar 序列和对应的可靠度
二 SSC 伪代码
SC 解码过程本质上跟决策树里面的ID3,C4.5一样的。
里面的beliefs本质上就是某个结点拿到的数据集
g,f函数就是如何划分数据集。
这边给出伪代码
至于为神马要用f,g函数,后面会有详细的推导过程、
# -*- coding: utf-8 -*-
"""
Created on Mon Mar 14 21:41:01 2022
@author: cxf
"""
import numpy as np
'''
阶梯函数
'''
def sgn(x):
r = 1
if x>=0:
r=1
else:
r=-1
return r
class Polar():
'''
实现f 函数功能
'''
def f(self, r1,r2):
beliefs = sgn(r1)*sgn(r2)*min(abs(r1),abs(r2))
return beliefs
'''
实现g 函数功能
'''
def g(self, r1,r2,hat_u):
if hat_u ==0: #作为g 函数
beliefs= r2+r1
else:
beliefs = r2-r1
return beliefs
'''
叶节点计算
'''
def getLeaf(self,tree, beliefs):
is_frozen = tree.isfrozen()
if is_frozen:
hat_u = 0
elif beliefs>=0:
hat_u =0
else:
hat_u =1
return hat_u
'''
左子树计算过程,step_R
'''
def getLeft(self,beliefs, tree, hat_u):
sub_beliefs =[]
n = len(beliefs)
if tree.isLeaf:#叶节点
hat_u = self.getLeaf(tree, beliefs)
else:
for i in range(n):
r1=beliefs[i]
r2 = beliefs[i+n]
u = hat_u[i]
belief = self.g(r1,r2,u)
sub_beliefs.append(belief)
hat_u = self.decoder(tree, sub_beliefs)
return hat_u
'''
右子树的计算过程
'''
def getRight(self, beliefs, tree):
sub_beliefs =[]
n = len(beliefs)
if tree.isLeaf:
hat_u = self.getLeaf(tree, beliefs)
else:
for i in range(n):
r1=beliefs[i]
r2 = beliefs[i+n]
belief = self.f(r1,r2)
sub_beliefs.append(belief)
hat_u = self.decoder(tree, sub_beliefs)
return hat_u
def transfer(self,tree,u1,u2):
n = len(u1)
x= []
x_2= u2
for i in range(n):
x1= u1[i]
x2 = u2[i]
a = x1^x2
x.append(a)
x.extend(x_2)
def decoder(self, tree,beliefs):
hat_u_1 = self.getLeft(beliefs, tree)
hat_u_2 = self.getRight(beliefs, tree)
self.transfer(tree, hat_u_1, hat_u_2)
def __init__(self):
self.N = 16
self.k = 10
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/24590.html