大家好，欢迎来到IT知识分享网。

返回 我的研究方向(Research Interests)

在网络科学研究中,鲁棒性是一个重要课题。互联网的前身ARPANET的一个目的就是为了构造能够在部分节点或连边失效时在剩余节点之间仍然能够维持基本通信的网络系统。

从图论的术语看,这就归结为如下问题:
如果在一个图G中去除了一些节点或者连边，那么图G中的两个给定顶点 s 和顶点 t 之间是否仍然存在路径(即是否仍然属于同一个连通片)?

这里先叙述图论中的 Menger定理，该定理是为了回答如下问题:
如果要使顶点 s 和顶点 t 分离(即分别属于不同的连通片)，那么至少需要从图G中去除多少个顶点?或者至少需要从图G中去除多少条边?

去除一个顶点对应着把以该顶点为端点之一的所有的边也去除。

以去除顶点为例，求解这一问题的自然的蛮力方法如下:

不包括顶点 s 和顶点 t 的话，图G中还有 N-2 个顶点。
首先看去除这 N-2 个顶点中的一个顶点是否有可能使得顶点 s 和顶点 t 分离，共有 N-2 种可能的去除方式;
如果不可能的话，那么再看去除这 N-2 个顶点中的两个顶点是否有可能使得顶点 s 和顶点 t 分离，共有\(C_{N-2}^{2}\)种可能的去除方式;
这样一直做下去，直到在某次去除 h 个顶点后使得顶点 s 和顶点 t 分离。

k 即为要使顶点 s 和顶点 t 分离所需去除的最少的顶点数目。

显然，对于较大规模的图，这一蛮力算法的计算量是非常大的。

而 Menger定理 给出了求解这一问题的一个有效方法，关于该定理的证明可参见图论著作。

Menger定理

点形式

设顶点 s 和顶点 t 为图 G 中两个不相邻的顶点，则使顶点 s 和顶点 t 分别属于不同的连通片所需去除的 顶点 的最少数目等于连接顶点 s 和顶点 t 的独立的简单路径的最大数目。

边形式

设顶点 s 和顶点 t 为图 G 中两个不同的顶点，则使顶点 s 和顶点 t 分别属于不同的连通片所需去除的 边 的最少数目等于连接顶点 s 和顶点 t 的 不相交 的简单路径的最大数目。

解释定理：
先对定理中的术语给出解释。两个顶点称为是不相邻的，是指这两个顶点之间没有边直接相连。
如果顶点 s 和顶点 t 为相邻顶点(即两者之间有边直接相连)，那么即使把图 G 中所有其他的顶点都去除也无法使这两个顶点分别属于不同的连通片。
这就是定理的点形式中假设两个顶点不相邻的原因。

连接顶点 s 和顶点 t 的两条简单路径称为是独立的，是指这两条路径的公共顶点只有顶点 s 和顶点 t 。连接顶点 s 和顶点 t 的两条简单路径称为是不相交的，是指这两条路径没有经过一条相同的边(但可以有共同顶点)。

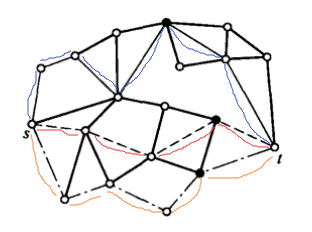
例如，在下图中，至少要去除3个顶点(标记为实心圆点)才能使得顶点 s 和顶点 t 分别属于不同的连通子图，从顶点 s 到顶点 t 也恰好有 3 条独立的简单路径(分别用不同线型标记)。

点割集( Vertex cutset)

使得一对顶点分属于不同的连通片所需去除的一组顶点称为这对顶点的点割集( Vertex cutset)。

边割集( Edge cutset)

使得一对顶点分属于不同的连通片所需去除的一组边称为这对顶点的边割集( Edge cutset)。

极小割集(Minimum cut set)

包含顶点数或边数最少的割集称为极小割集(Minimum cut set)。

基于Menger定理，为了计算使顶点 s 和顶点 t 分离所需要去除的顶点的最少数目，我们只需要求出顶点 s 和顶点 t 之间所有的简单路径，而对于后者存在一个经典的有效算法—Dijkstra算法。

参考：

[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012