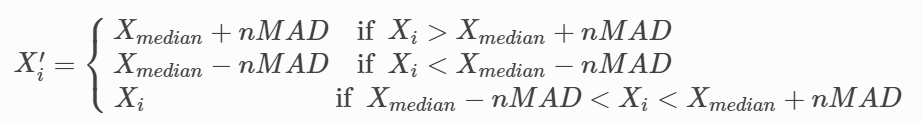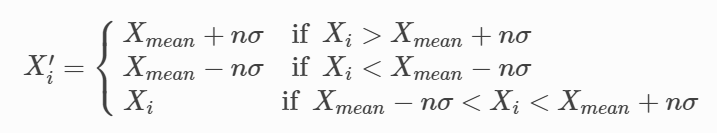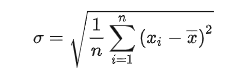数据挖掘-报告 细说 离群值处理

大家好，欢迎来到IT知识分享网。

最近在弄这个 需要弄明白这些原理 

我要知道为什么要这么做 如何做 有什么类型 如何对比做了前后

然后加到报告里

包含part：原理 处理前 处理后

大多数的参数统计数值，如均值、标准差、相关系数 等，以及基于这些参数的统计分析，均对离群值高度敏感。因此，离群值的存在会对数据分析造成极大影响。

离群值(outlier)，也称逸出值，是指在数据中有一个或几个数值与其他数值相比差异较大。chanwennt准则规定，如果一个数值偏离观测平均值的概率小于等于1/(2n)，则该数据应当舍弃（其中n为观察例数，概率可以根据数据的分布进行估计）。当遇到一组数据中有少量outliers,一般需要删除掉，避免对正确的结果造成干扰。我们可以通过箱线图来检测并去除outliers。下面小编通过定义两种不同的函数来处理离群值。

1. MAD法：

MAD又称为绝对值差中位数法（Median Absolute Deviation）。MAD 是一种先需计算所有因子与平均值之间的距离总和来检测离群值的方法　　

处理的逻辑：第一步，找出所有因子的中位数 Xmedian；第二步，得到每个因子与中位数的绝对偏差值 Xi−Xmedian；第三步，得到绝对偏差值的中位数 MAD；最后，确定参数 n，从而确定合理的范围为 [Xmedian−nMAD,Xmedian nMAD]，并针对超出合理范围的因子值做如下的调整：

2. 3σ法

又称为标准差法。标准差本身可以体现因子的离散程度，是基于因子的平均值 Xmean而定的。在离群值处理过程中，可通过用 Xmean±nσ来衡量因子与平均值的距离。　　

标准差法处理的逻辑与MAD法类似，首先计算出因子的平均值与标准差，其次确认参数 n（这里选定 n = 3），从而确认因子值的合理范围为 [Xmean−nσ,Xmean nσ]，并对因子值作如下的调整：

对比展示 画图 画那个偏态 数据分布图

处理前 处理后的图放到同一张图里

通常，在其余数据上做各种假设，并且证明检测到的离群点显著违反了这些假设。如统计学中的假设检验，基于小概率原理，对原假设进行判断。一般检测离群点，是人工进行筛选，剔除不可信的数据，例如对于房屋数据，面积上万，卧室数量过百等情况。而在面对大量的数据时，人工方法耗时耗力，因此，才有如下的方法进行离群点检测。

【1】基于统计模型的方法：

首先建立一个数据模型，异常是那些同模型不能完美拟合的对象；

如果模型是簇的集合，则异常是不显著属于任何簇的对象；

在使用回归模型时，异常是相对远离预测值的对象。

【2】基于邻近度的方法：通常可以在对象之间定义邻近性度量，异常对象是那些远离其他对象的对象。

【3】基于密度的方法：仅当一个点的局部密度显著低于它的大部分近邻时才将其分类为离群点。

【4】基于聚类的方法：聚类分析用于发现局部强相关的对象组，而异常检测用来发现不与其他对象强相关的对象。因此，聚类分析非常自然的可以用于离群点检测。

 还有99.7%的数值位于3个标准差的范围以内

1.基于正态分布的一元离群点检测

当数据服从正太分布的假设时在正态分布的假定下，u±3σ区域包含99.7%的数据，u±2σ包含95.4%的数据，u±1σ包含68.3%的数据。其区域外的数据视为离群点。

 处理逻辑 默认 训练的数据是符合正态分布的 delta

需要基于此原理 将区域外的数据进行离群处理 某些X与Y差 也符合

标准差公式：反应数据的离散程度

 标准差比平均差更能反映数据的离散度

误差分布——正态分布（描述偶然误差通常用正态分布，其特性：在一定观测条件下，误差的绝对值有一定的限制，或者说，超出一定限制的误差，其出现的概率为零；绝对值较小的误差比绝对值较大的误差出现的概率大；绝对值相等的正负误差出现的概率相同；偶然误差的数学期望为零），并用最小二乘法加以验证。

就是那些远离绝大多数样本点的特殊群体，通常这样的数据点在数据集中都表现出不合理的特性。如果忽视这些异常值，在某些建模场景下就会导致结论的错误

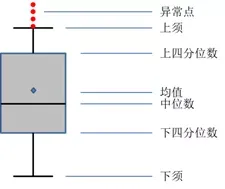
箱线图技术实际上就是利用数据的分位数识别其中的异常点，该图形属于典型的统计图形，在学术界和工业界都得到广泛的应用。箱线图的形状特征如下图所示：