大家好，欢迎来到IT知识分享网。

题目链接

题目描述

给定一颗n个点n−1条边的树，每条边的长度都是1，i号节点的权是\(a_i\)。如果三个节点两两在树上的距离都是4，那么称这三个节点构成了一个“组合”，一个“组合”的权是三个节点的权的乘积。求所有“组合”的权的和。

数据范围：$$1\le n\le 10^{5} , 1\le a_i \le 10$$

题目分析

• 1

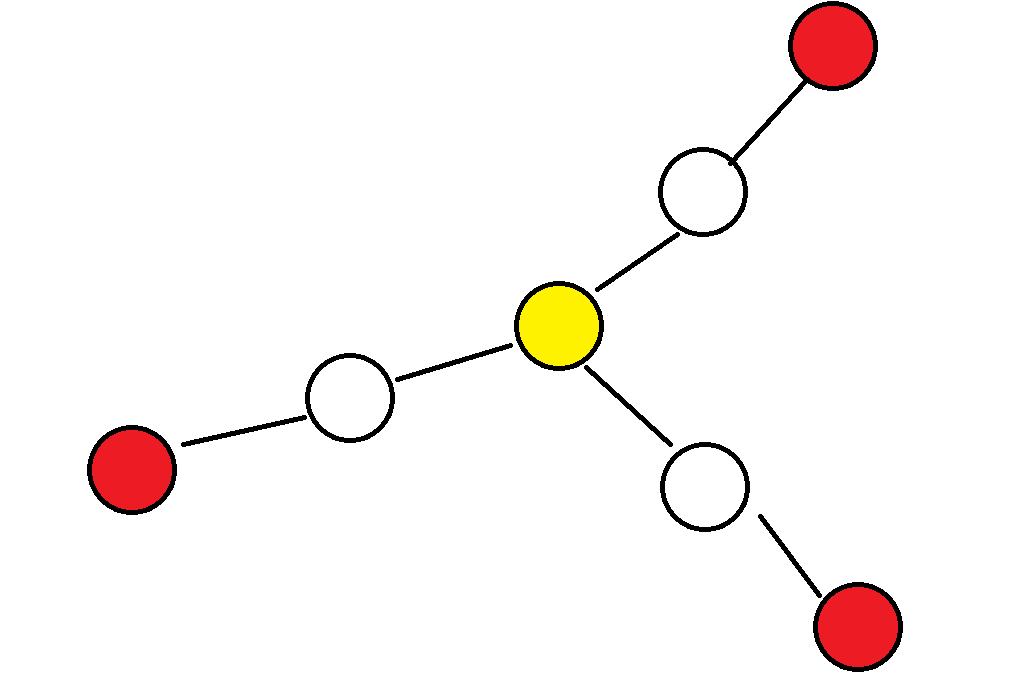
  直觉上，一个组合中的点一定是这种形状（红色点）：
  
  下面证明：
  设三个点为A,B,C。记d(x,y)为x到y的距离,记A到B与B到C的路径的重叠部分长为t。
  由于树上两点间简单路径是唯一的，所以$$d(A,C)=d(A,B)+d(B,C)-2t$$
  $$t=2$$
  Q.E.D

• 2

  定义上图中黄点为组合的中心点。
  显然
  以一个点为中心点的所有组合的权值之和 即 到此点距离为2的点的集合 的 三元子集 的权值之和

• 3

  根据这道题 ,我们有O(n)的方法求出一个集合的三元子集的权值之和

• 4

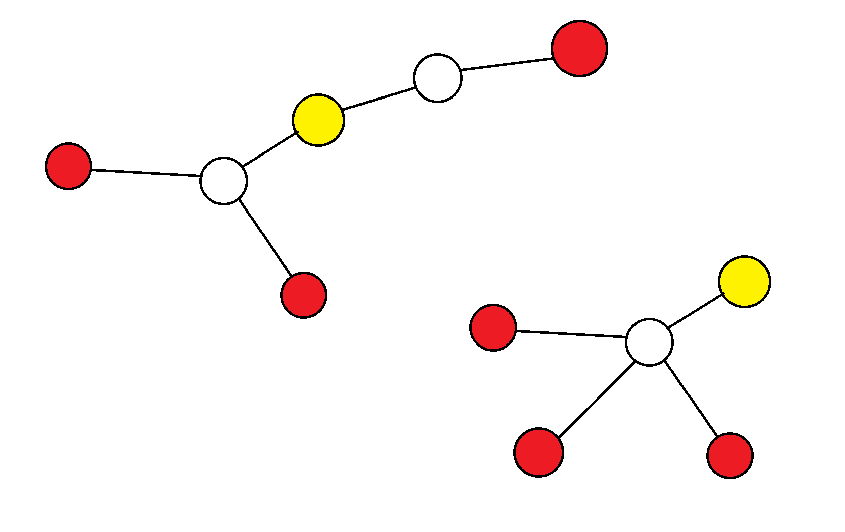
  前面的算法会将如下图的三个点视为一个组合，于是需要减去
  

代码（没过）

• 快读&邻接表等一堆废话

int n;
long long ans;
int pw[MAXN],head[MAXN],to[MAXN<<1],nxt[MAXN<<1],cnt;
inline void add(int a,int b){
    ++cnt;
    to[cnt]=b;
    nxt[cnt]=head[a];
    head[a]=cnt;
    return ;
}
inline int read(){
    int x=0;char c;
    c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9'){
        x=x*10+c-'0';
        c=getchar();
    }
    return x;
}

• 求与中心点距离为2的点

  使用两个队列，算法类似bfs

for(int j=head[i];j;j=nxt[j]) q1.push(to[j]); //q1存距离为1的点
while(!q1.empty()){
      now=q1.front();q1.pop();
      for(int j=head[now];j;j=nxt[j]){
            if(to[j]==i) continue;
            q2.push(to[j]); //q2存距离为2的点
      }
}

• 求三元组的和

  此处可以参考这篇题解

for(c=1;!q2.empty();++c){
            s[0][c]=pw[q2.front()];q2.pop(); //把点从队列里取到数组里
        }
        --c;
        s[1][0]=s[2][0]=s[3][0]=0;
        for(int i=1;i<=c;++i) s[1][i]=s[1][i-1]+s[0][i]; //一元组的和 前缀和
        for(int i=1;i<=c;++i) s[2][i]=s[2][i-1]+s[1][i-1]*s[0][i]; //二元组的和
        for(int i=1;i<=c;++i) s[3][i]=s[3][i-1]+s[2][i-1]*s[0][i];

• 总代码

#include<iostream>
#include<queue>
#define MAXN 100005
using namespace std;
int n;
long long ans;
int pw[MAXN],head[MAXN],to[MAXN<<1],nxt[MAXN<<1],cnt;
inline void add(int a,int b){
    ++cnt;
    to[cnt]=b;
    nxt[cnt]=head[a];
    head[a]=cnt;
    return ;
}
inline int read(){
    int x=0;char c;
    c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9'){
        x=x*10+c-'0';
        c=getchar();
    }
    return x;
}
queue<int> q1,q2;
int s[4][MAXN];
int main(){
    n=read();
    for(int i=1;i<=n;++i) pw[i]=read();
    int a,b;
    for(int i=1;i<n;++i){
        a=read(),b=read();
        add(a,b);
        add(b,a);
    }
    int c,now;
    for(int i=1;i<=n;++i){
        while(!q2.empty()) q2.pop();
        for(int j=head[i];j;j=nxt[j]) q1.push(to[j]);
        while(!q1.empty()){
            now=q1.front();q1.pop();
            for(int j=head[now];j;j=nxt[j]){
                if(to[j]==i) continue;
                q2.push(to[j]);
                //cout<<"!"<<to[j]<<endl;
            }
            //cout<<"!"<<now<<endl;
        }
        for(c=1;!q2.empty();++c){
            s[0][c]=pw[q2.front()];q2.pop();
            //cout<<"?"<<s[0][i]<<endl;
        }
        --c;
        s[1][0]=s[2][0]=s[3][0]=0;
        for(int i=1;i<=c;++i) s[1][i]=s[1][i-1]+s[0][i]; //一元组的和 前缀和
        for(int i=1;i<=c;++i) s[2][i]=s[2][i-1]+s[1][i-1]*s[0][i]; //二元组的和
        for(int i=1;i<=c;++i) s[3][i]=s[3][i-1]+s[2][i-1]*s[0][i];
        //ans+=/*q2的三元组的和*/;
        ans+=s[3][c];
        //cout<<ans<<' '<<c<<endl;
    }
    cout<<ans;
    return 0;
}