大家好,欢迎来到IT知识分享网。
转载一篇关于DQN解释非常好的文章
转载自:https://zhuanlan.zhihu.com/p/46852675
本人做了一些细微的改动,方便个人理解,原文请点这里
DQN的由来和解释
Q-Learning可以很好的解决迷宫问题,但这终究是个小问题,它的状态空间和动作空间都很小。而在实际的情况下,大部分问题都有巨大的状态空间或动作空间,建立Q表,内存是不允许的,而且数据量和时间开销也是个问题。
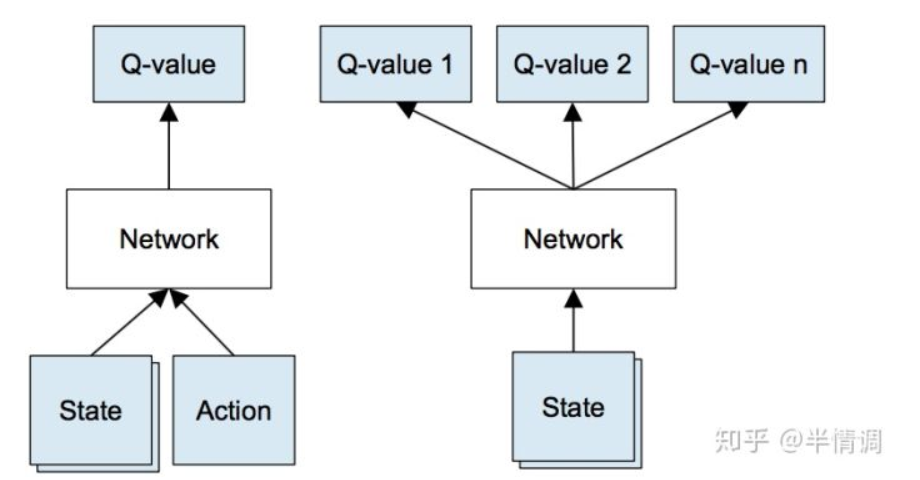
我们可以使用神经网络来表示我们的 Q 函数,每层网络的权重就是对应的值函数,取 4 四帧游戏图像作为 state,输出每个 action 对应的 Q 值。如果我们想要执行 Q 值的更新,或者选择具有最高 Q 值的对应的 action,我们只需经过整个网络一次就能立刻获得任意动作对应的 Q 值。DQN的原始输入为连续的4帧图像,不只使用一帧画面是为了感知环境的动态性。
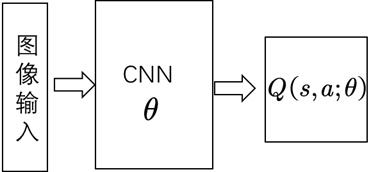
左图:简单的DQN模型,右图:DeepMind改进的DQN模型
假设一帧图像有84个像素点,那么四帧图像就有84*84*4个像素。每一个像素点的取值是0-255可能,所有的可能性就有256^(84*84*4)。
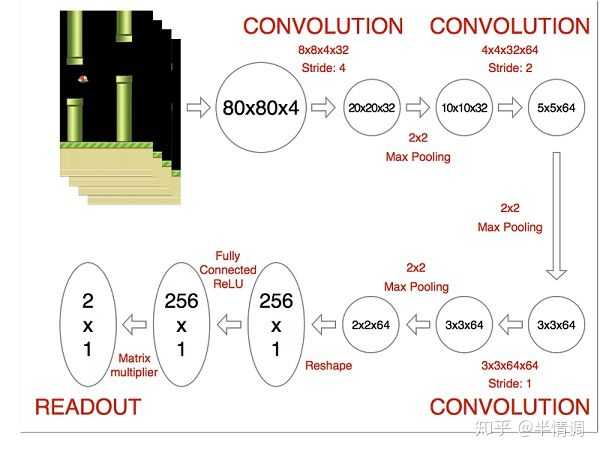
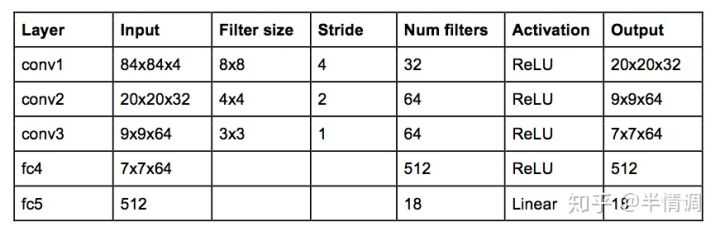
DeepMind使用的网络结构如下:
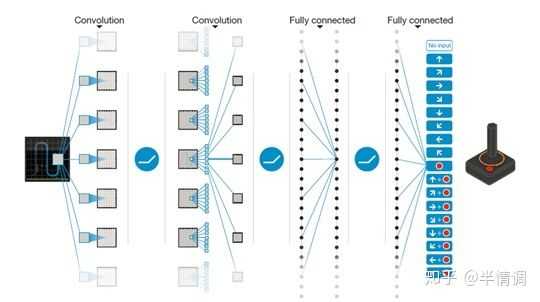
这是一个经典的带有三层卷积层的卷积神经网络,后面跟两个全连接层。注意:这里没有池化层,池化层会让你获得平移不变性,即网络对图像中对象的位置变得不敏感。这对于 ImageNet 这样的分类任务来说是有意义的,但游戏中位置对潜在的奖励至关重要,我们不希望丢失这些信息。
这个网络的输入是4个84 x 84 的灰度游戏屏幕,输出是每个可能的动作对应的 Q 值 (DeepMind 实验玩的游戏是 Atari,对应有 18 种动作)。这成为一个回归任务,可以用简单的平方误差损失进行优化:
L = 1 2 [ r + max a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] 2 L=\frac{1}{2}[r + \max _{a’} {\mathcal {Q}}(s’,a’) – \mathcal {Q}(s,a) ]^{2} L=21[r+a′maxQ(s′,a′)−Q(s,a)]2
对于给定的<s, a, r, s'>,前一算法的 Q表的更新规则应该做如下修改:
1.对当前状态 s 进行一次前馈,获得所有 action 预测的 Q 值。;
2.对下一个状态 s’ 进行一次前馈,计算整个网络最大的输出值 max a ′ Q ( s ′ , a ′ ) \max _{a’} {\mathcal {Q}}(s’,a’) maxa′Q(s′,a′)
3.为动作设置目标Q值 r + max a ′ Q ( s ′ , a ′ ) r+\max _{a’} {\mathcal {Q}}(s’,a’) r+maxa′Q(s′,a′) ;
4.通过反向传播更新权重。
DQN对Q-Learning的修改主要体现在三个方面:
(1)DQN利用深度卷积神经网络逼近值函数;
(2)DQN利用经验回放(experience replay)训练强化学习的学习过程;
(3)DQN独立设置了目标网络来单独处理时间差分算法中的TD偏差。
下面具体介绍:
(1)DQN利用深度卷积神经网络逼近值函数。此处的值函数对应着一组参数,在神经网络里参数是每层网络的权重,用θ表示,用公式表示的值函数Q(s,a;θ)。此时更新值函数时其实是更新参数θ,当神经网络确定时,θ就表示值函数。
第一个DQN模型
(2)经验回放的动机是:①深度神经网络作为有监督学习模型,要求数据满足独立同分布;②通过强化学习采集的数据之间存在着关联性,利用这些数据进行顺序训练,神经网络表现不稳定,而经验回放可以打破数据间的关联。
在强化学习过程中,智能体将数据存储到一个数据库中,再利用均匀随机采样的方法从数据库中抽取数据,然后利用抽取的数据训练神经网络(13年的NIPS中已提出)。
经验回放
(3)利用神经网络对值函数进行逼近时,值函数的更新步更新的是参数θ,更新方法是梯度下降法。因此值函数更新实际上变成了监督学习的一次更新过程,其梯度下降法为:
θ t + 1 = θ t + α [ r + γ max a ′ Q ( s ′ , a ′ ; θ ) − Q ( s , a , θ ) ] ∇ Q ( s , a ; θ ) \theta_{t+1}=\theta_t+\alpha\big[r+\gamma\max _{a’} {\mathcal {Q}}(s’,a’;\theta)- \mathcal {Q}(s,a,\theta)\big]\nabla \mathcal {Q}(s,a;\theta) θt+1=θt+α[r+γa′maxQ(s′,a′;θ)−Q(s,a,θ)]∇Q(s,a;θ)
r + γ max a ′ Q ( s ′ , a ′ ; θ ) r+\gamma\max _{a’} {\mathcal {Q}}(s’,a’;\theta) r+γmaxa′Q(s′,a′;θ)为TD目标,在计算 max a ′ Q ( s ′ , a ′ ; θ ) \max _{a’} {\mathcal {Q}}(s’,a’;\theta) maxa′Q(s′,a′;θ) 值时用到的网络参数为 θ \theta θ 。
我们称计算TD目标时所用的网络为TD网络。以往的神经网络逼近值函数时,计算TD目标的动作值函数所用的网络参数 θ \theta θ ,与梯度计算中要逼近的值函数所用的网络参数相同,这样就容易使得数据间存在关联性,训练不稳定。为了解决这个问题,DeepMind提出计算TD目标的网络参数表示为 θ − \theta^{-} θ− ;计算值函数逼近的网络参数表示为 θ \theta θ;用于动作值函数逼近的网络每一步都更新,而用于计算TD目标的网络每个固定的步数更新一次。
计算TD目标的网络就是
TargetNet
计算值函数逼近的就是MainNet
因此值函数的更新变为: θ t + 1 = θ t + α [ r + γ max a ′ Q ( s ′ , a ′ ; θ − ) − Q ( s , a , θ ) ] ∇ Q ( s , a ; θ ) \theta_{t+1}=\theta_t+\alpha\big[r+\gamma\max _{a’} {\mathcal {Q}}(s’,a’;\theta^-)- \mathcal {Q}(s,a,\theta)\big]\nabla \mathcal {Q}(s,a;\theta) θt+1=θt+α[r+γmaxa′Q(s′,a′;θ−)−Q(s,a,θ)]∇Q(s,a;θ)
DQN的伪代码
DQN伪代码
第[1]行,初始化回放记忆D,可容纳的数据条数为N
第[2]行,利用随机权值 θ \theta θ 来初始化动作-行为值函数Q
第[3]行,令 θ − = θ \theta^-=\theta θ−=θ 初始化用来计算TD目标的动作行为值Q
第[4]行,循环每次事件
第[5]行,初始化事件的第一个状态s1 ,预处理得到状态对应的特征输入
第[6]行,循环每个事件的每一步
第[7]行,利用概率 ε \varepsilon ε 选一个随机动作 a t a_t at
第[8]行,如果小概率事件没发生,则用贪婪策略选择当前值函数最大的那个动作:
a t = a r g max a Q ( ϕ ( s t ) , a , θ ) a_t=arg\max_aQ(\phi \left( s_t \right),a,\theta) at=argamaxQ(ϕ(st),a,θ)
注意,这里选最大动作时用到的值函数网络与逼近值函数所用的网络是一个网络,都对应着 θ \theta θ 。
注意:第[7]行和第[8]行是行动策略,即 ε − g r e e d y \varepsilon -greedy ε−greedy策略。
第[9]行,在仿真器中执行动作 a t a_t at ,观测回报 r t r_t rt以及图像 x t + 1 x_{t+1} xt+1.
第[10]行,更新 s t + 1 = s t s_{t+1}=s_t st+1=st,设置 a t , x t + 1 a_t,x_{t+1} at,xt+1,预处理 ϕ t + 1 = ϕ ( s t + 1 ) \phi _{t+1}=\phi (s_{t+1}) ϕt+1=ϕ(st+1)
第[11]行,将转换结果 ( ϕ t , a t , r t , ϕ t + 1 ) (\phi _{t},a_t,r_t,\phi_{t+1}) (ϕt,at,rt,ϕt+1) 储存在回放记忆D中
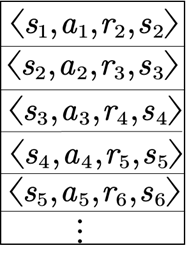
第[12]行,从回放记忆D中均匀随机采样一个转换样本数据,用 ( ϕ j , a j , r j , ϕ j + 1 ) (\phi _{j},a_j,r_j,\phi_{j+1}) (ϕj,aj,rj,ϕj+1) 来表示。
第[13]行,判断是否是一个事件的终止状态,若是终止状态则TD的回报reward为 r j r_j rj ,否则利用TD目标网络参数 θ − \theta^- θ− 计算TD回报(reward): r + γ max a ′ Q ( s ′ , a ′ ; θ − ) r+\gamma\max _{a’} {\mathcal {Q}}(s’,a’;\theta^-) r+γmaxa′Q(s′,a′;θ−) 。
第[14]行,执行一次梯度下降算法:
Δ θ = α [ r + γ max a ′ Q ( s ′ , a ′ ; θ − ) − Q ( s , a , θ ) ] ∇ Q ( s , a ; θ ) \varDelta\theta=\alpha\big[r+\gamma\max _{a’} {\mathcal {Q}}(s’,a’;\theta^-)- \mathcal {Q}(s,a,\theta)\big]\nabla \mathcal {Q}(s,a;\theta) Δθ=α[r+γa′maxQ(s′,a′;θ−)−Q(s,a,θ)]∇Q(s,a;θ)
第[15]行,更新动作值函数逼近的网络参数 θ = θ + Δ θ \theta=\theta+\varDelta\theta θ=θ+Δθ
第[16]行,每隔C步更新一次TD目标网络权值即令 θ − = θ \theta^-=\theta θ−=θ
第[17]行,结束每次事件内循环
第[18]行,结束事件间的循环
我们可以看到,在第[12]行,利用了经验回放;在[13]行利用了独立的目标网络 θ − \theta^- θ−;第[15]行,更新动作值函数逼近网络参数;第[17]行更新目标网络参数.
参考:
1.揭秘深度强化学习神经网络(DQN)
2.天津包子馅儿:深度强化学习系列 第一讲 DQN
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/10094.html