大家好，欢迎来到IT知识分享网。

1. 线性整流单元（Rectified Linear Unit, ReLU）简介

在神经网络中，激活函数负责将来自节点的加权总和输入转换为节点或该输入的输出的激活。ReLU激活函数是分段线性函数，如果为正，将直接输出输入，否则将输出零。它已成为许多类型的神经网络的默认激活功能，因为使用该模型的模型更易于训练，并且通常可以获得更好的性能。

1.1 Sigmoid和Tanh激活函数的局限性

神经网络由节点层组成，并学习输入到输出的映射。对于给定的节点，将输入乘以节点中的权重，再求和，此值称为节点的总激活量。然后，通过激活函数对求和的激活进行转换，并定义节点的特定输出或“激活”。

最简单的激活函数称为线性激活，其中根本不应用任何变换。仅包含线性激活函数的网络很容易训练，但无法学习复杂的映射函数。线性激活函数仍在输出层中用于预测数量的网络（例如回归问题）。

首选非线性激活函数，因为它们允许节点学习数据中更复杂的结构。传统上，两个广泛使用的非线性激活函数是S形和双曲正切激活函数。

sigmoid激活函数，也称为logistic函数，传统上是神经网络非常流行的激活函数。该函数的输入将转换为0.0到1.0之间的值。远大于1.0的输入将转换为值1.0，类似地，远小于0.0的值将捕捉为0.0。长期以来，直到1990年代初，它都是神经网络使用的默认激活函数。

双曲正切函数（tanh）是形状相似的非线性激活函数，其输出值介于-1.0和1.0之间。在1990年代后期和整个2000年代，tanh函数优于S型激活函数，因为使用该模型更容易训练，并且通常具有更好的预测性能。

S型和tanh函数的一个普遍问题是饱和（saturation）。这意味着tanh和Sigmoid的大值分别捕捉为1.0，小值捕捉为-1或0。此外，这些功能仅对输入中点附近的变化非常敏感，例如S型为0.5，tanh为0.0。无论输入提供的节点的总激活数是否包含有用信息，较低的灵敏度。一旦饱和，对于学习算法而言，继续调整权重以改善模型的性能变得具有挑战性。

随着GPU算力的增强，可以训练非常深的神经网络，但使用S形和tanh激活函数的网络变得不容易训练。使用这些非线性激活函数的大型网络中的深层无法接收有用的梯度信息。错误会通过网络传播回来，并用于更新权重。给定所选激活函数的导数，误差的传播量随传播层的增加而显着降低，这被称为梯度消失（vanishing gradient），并阻止有效地学习深度（多层）网络。消失的梯度使得很难知道参数应朝哪个方向移动以改善损失函数（loss function）。

1.2 ReLU激活函数

为了使用带有误差的反向传播的随机梯度下降来训练深度神经网络，需要一个看起来像线性函数的函数，但实际上是一个非线性函数，可以学习数据中的复杂关系。该函数还必须对激活总和输入提供更高的灵敏度，并避免轻易的饱和。

实现此激活功能的节点或单元称为线性整流单元（Rectified Linear Unit, ReLU）。通常，将整流器功能用于隐藏层的网络称为整流网络。采用ReLU可以很容易地被认为是深度学习革命中的几个里程碑之一，例如，现在可以使用ReLU开发非常深的神经网络。

简单的描述：

if input > 0:
	return input
else:
	return 0

简单的实现：

# rectified linear function
def rectified(x):
	return max(0.0, x)

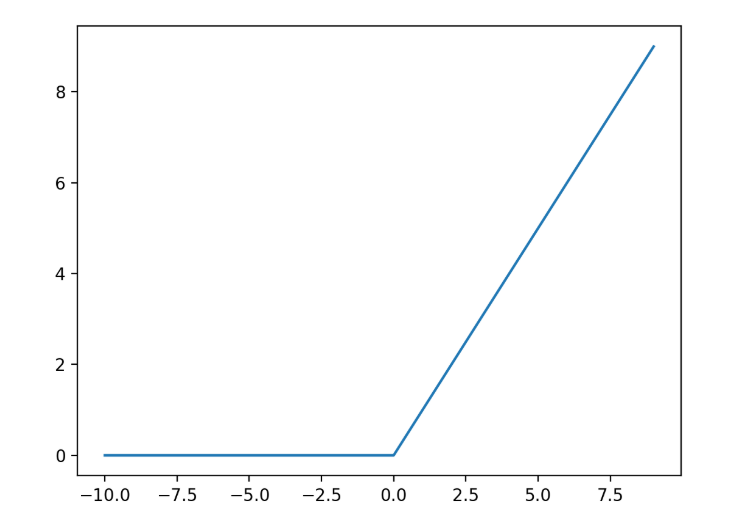
绘图：

# plot inputs and outputs
from matplotlib.pyplot import plt

# rectified linear function
def rectified(x):
	return max(0.0, x)

# define a series of inputs
series_in = [x for x in range(-10, 11)]
# calculate outputs for our inputs
series_out = [rectified(x) for x in series_in]
# line plot of raw inputs to rectified outputs
plt.plot(series_in, series_out)
plt.show()

整流线性函数的导数也很容易计算。在更新节点的权重作为错误的反向传播的一部分时，需要激活函数的导数。函数的导数是斜率。负值的斜率是0.0，正值的斜率是1.0。

2. ReLU 激活函数的优点

2012年，ReLU首先由Xavier Glorot等人着重指出，论文《Deep Sparse Rectifier Neural Networks》。

2.1 计算简单

无需在激活中计算指数函数，这与需要使用指数计算的tanh和Sigmoid激活函数不同。

2.2 稀疏性表示（Representational Sparsity）

ReLU的一个重要优势是它能够输出真正的零值。这与tanh和Sigmoid激活函数不同，后者学习近似零输出，例如非常接近零的值，但不是真正的零值。

这意味着负输入可以输出真实零值，从而允许神经网络中的隐藏层激活以包含一个或多个真实零值。这称为稀疏表示，是表示学习的理想属性，因为它可以加快学习速度并简化模型。

在自动编码器中，研究和寻求诸如稀疏性之类的有效表示的领域是，在网络从紧凑表示重新构造输入之前，网络学习了输入的紧凑表示（称为代码层），例如图像或序列。

2.3 线性性质

ReLU激活函数的函数图像正半轴类似于线性激活功能。通常，当神经网络的行为为线性或接近线性时，更易于优化。此属性的关键在于，使用此激活函数训练的网络几乎完全避免了梯度消失的问题，因为梯度保持与节点激活成比例。

2.4 训练深度神经网络

深整流器网络（deep rectifier networks）可以达到最佳性能，而无需对带有大型标签数据集的纯监督任务进行任何未经监督的预培训。因此，这些结果可以看作是尝试理解训练深层但纯监督的神经网络的难度，并缩小在有无监督的预训练和无监督的情况下学习的神经网络之间的性能差距。

3. 使用ReLU的技巧

3.1 使用ReLU作为默认的激活函数

在引入ReLU之前，大多数神经网络都使用逻辑Sigmoid激活函数或tanh激活函数。现代深度学习神经网络，默认激活函数是整流线性激活函数。

3.2 ReLU适合MLP，CNN，可能不适合RNN

将ReLU与CNN一起使用时，它们可以用作过filter map的激活函数，然后是池化层。卷积网络的典型层包括三个阶段。在第二阶段，每个线性激活都通过非线性激活函数（例如ReLU激活函数）运行。该阶段有时称为检测器阶段（detector stage）。

传统上，LSTM使用tanh激活函数来激活单元状态，并使用S型激活函数来输出节点。考虑到他们的精心设计，默认情况下，ReLU被认为不适用于循环神经网络（RNN），例如长短期记忆网络（LSTM）。

尽管如此，仍在研究将ReLU用作LSTM中的输出激活的一些工作，其结果是对网络权重进行了仔细的初始化，以确保训练之前网络是稳定的。在2015年题为A Simple Way to Initialize Recurrent Networks of Rectified Linear Units的论文中对此进行了概述。

3.3 使用较小的偏置

偏差是具有固定值的节点上的输入。偏置具有改变激活功能的作用，并且传统上将偏置输入值设置为1.0。在网络中使用ReLU时，请考虑将偏差设置为较小的值，例如0.1。将[bias]的所有元素设置为较小的正值（例如0.1）是一种好习惯。这使得整流线性单位很可能最初对训练集中的大多数输入有效，并允许导数通过。

3.4 使用何恺明权重初始化

在训练神经网络之前，必须将网络的权重初始化为较小的随机值。在网络中使用ReLU并将权重初始化为以零为中心的较小随机值时，默认情况下，网络中一半的单位将输出零值。在权重统一初始化之后，约50％的隐藏单位连续输出值是零。

有许多启发式方法可以初始化神经网络的权重，但是没有最佳的权重初始化方案，除了将权重初始化方案映射到激活函数的选择的一般准则之外，关系不大。

Glorot和Bengio建议采用适当缩放的均匀分布进行初始化。这称为Xavier初始化。它的推导基于激活是线性的假设。该假设对ReLU无效

何恺明等人提出了Xavier初始化的小修改，使其适合与ReLU一起使用，现在通常称为“ he initialization ”；keras中指定方法为：【kernel_initializer='he_uniform'】

3.5 标准化输入数据

如果没有在许多问题上进行数据缩放，神经网络的权重可能会增大，从而使网络变得不稳定并增加泛化误差。

常用方法 Z-Score方法，减去均值，除以标准差。

3.6 使用正则化

由于ReLU的输出在正域内不受限制，可能会引起另一个问题。因此，需要使用正则化来防止潜在的数值问题。在激活值上使用L1惩罚，促进了额外的稀疏性。这既是促进稀疏表示（例如使用L1正则化）又可以减少模型的泛化误差的好习惯。

3.7 ReLU的扩展

3.7.1 LReLU

LReLU（Leaky ReLU，LReLU），修改了ReLU函数，以在输入小于零时允许较小的负值。当单元饱和且不工作时，漏泄式整流器允许一个小的非零梯度。

Rectifier Nonlinearities Improve Neural Network Acoustic Models

3.7.2 PReLU

参数化线性整流单元（The Parametric ReLU，PReLU），该激活函数可自适应地学习整流器的参数。

【paper】Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification

3.7.3 ELU

指数线性单位（The Exponential Linear Unit，ELU）是ReLU的概括，它使用参数化的指数函数从正值过渡到小的负值。ELU具有负值，这将激活的平均值推近零。接近零的均值激活可以使学习更快，因为它们使梯度更接近自然梯度。

【paper】Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)

3.7.4 Maxout

Maxout是可替代的分段线性函数，它返回输入的最大值，该函数设计为与Dropout正则化技术结合使用。之所以这样命名，是因为其输出是一组输入的最大值，并且因为它适合与Dropout一起使用，旨在通过dropout促进优化，并提高dropout的快速近似模型平均精度的技术。

参考：
https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/