大家好，欢迎来到IT知识分享网。

1 数理统计基本概念

1.1 总体 $X$

  在数理统计中，我们往往研究有关对象的某一项数量指标（例如，研究某种灯泡的寿命，这一数量指标）。为此，考虑与这一数量指标相联系的随机试验，对这一数量指标进行实验或观察。我们将实验全部可能的观察值称为 总体，即：所研究对象的全部个体（数据）的集合。这些数值不一定都不相同，数目上也不一定是有限的，每一个可能观察值称为 个体。总体中所包含的个体数量称为总体的 容量。容量为有限的称为 有限总体；容量为无限的称为 无限总体。
  例如，考察某大学，一年级男生的身高，若一年级男生人数为2000人，每个男生的身高是一个可能观察值，共2000个可能观察值，是一个有限总体。又例如，考察一湖泊任意地点的深度（平面上有无数多的点），所得总体为无限总体。
  因为总体中的个体都是随机实验的一个观察值，因此可以看作某一随机变量$X$的值，这样，一个总体对应于一个随机变量$X$。我们对一个总体的研究就是对一个随机变量$X$的研究，$X$的分布函数与数字特征就称为总体的分布函数和数字特征。笼统的称为总体$X$。
  例如，检验零件的好坏，以0代表正品，1代表次品。设出现次品的概率为$p$（常数），那么总体就由一些”0″和”1″组成，这个总体对应（0-1）分布 P { X = x } = p x ( 1 − p ) 1 − x ,    x = 0 , 1 P\{X=x\}=p^x(1-p)^{1-x},\ \ x=0,1 P{
X=x}=px(1−p)1−x,  x=0,1的随机变量。

1.2 简单随机样本

  在实际中，总体分布一般是未知的。在数理统计中，都是通过从总体中抽取一部分个体，根据获取的数据来对总体分布做出推断，被抽取的这部分个体叫做样本。样本 是按照一定的规则从总体中抽样出来的一部分个体，所谓 “按照一定的规则” 是指总体中的每一个个体均有同等被抽出的机会。即相同条件下，对总体$X$进行相同的，独立的观察并记录结果。将$N$次观察的结果按实验的次序记为$x_1,x_2,\cdots ,x_N$，无特别说明样本都指简单随机样本。也可以说$N$个独立且与总体$X$同分布的随机变量$X_1,X_2,\cdots ,X_N$，他们对应的观察值$x_1,x_2,\cdots ,x_N$称为样本值。将样本看成一个随机变量，写成$(X_1,X_2,\cdots ,X_N)$，此时样本观察值写成$(x_1,x_2,\cdots ,x_N)$。

【注】样本的性质与维度问题：

• 样本是独立同分布的，分布函数表示为$F(x_1,x_2,\cdots ,x_N)=F(x_1)F(x_2)\cdots F(x_N)={\prod }_{i=1}^{N}F(x_i)$；概率密度为$f(x_1,x_2,\cdots ,x_N)=f(x_1)f(x_2)\cdots f(x_N)={\prod }_{i=1}^{N}f(x_i)$；
• 根据研究对象的不同，样本$(X_1,X_2,\cdots ,X_N)$中的一个样本$X_i$可以为任意维度的随机变量。在具体的一次观测或实验中，得到一组对应相同维度的具体数值$x_1,x_2,\cdots ,x_N$，称为样本的观察值或样本值。例如，考察某学校男生身高，则每次观察只需要记录男生身高就行，此时样本为一维数据；再例如考察某地方的环境指标，每次观测会记录该地点的水文，气象等多个值，此时样本为多维数据。有时为便于区分，将样本的观察值记为$(x_1,x_2,\cdots ,x_N)$，即可以理解为在抽样之前或理论研究时，$(X_1,X_2,\cdots ,X_N)$为随机变量；在抽样之后或实际应用时，$(x_1,x_2,\cdots ,x_N)$为观察值，本质上说的是一回事。

1.3 统计量

  样本$X_1,X_2,\cdots ,X_N$，不含任何（与总体有关的）未知参数的函数$g(X_1,X_2,\cdots ,X_N)$称为统计量。
常见的统计量：
$$样本均值：\overline{X}=\frac{1}{N}\sum _{i=1}^N{X}_i$$ $$样本方差：S^2=\frac{1}{N-1}\sum _{i=1}^N(X_i-\overline{X}{)}^2=\frac{1}{N-1}\sum _{i=1}^N(X_i^2-N\overline{X})$$

1.4 样本均值与总体均值、样本方差与总体方差

  样本为从总体中抽样出来的个体，一般都是可数的，所以求样本均值时，直接用所有样本观察值之和除以样本个数即可。求样本均值也就是求平均值（$N$为样本个数），即：$$\overline{X}=\frac{1}{N}\sum _{i=1}^N{x}_i$$而总体的个数不一定是可数的，用上述的方式求总体的均值显然是不合适的。
  举个栗子，射击手进行打靶练习，规定射入区域 $e_2$ 得 $2$ 分，射入区域 $e_1$ 得 $1$ 分，射入区域 $e_0$ 得 $0$ 分，射击手一次射击得分数 $X$ 是一个随机变量。

设 $X$ 的分布率为 P { X = k } = p k ,    k = 0 , 1 , 2 P\{ X=k\}=p_k,\ \ k=0,1,2 P{
X=k}=pk​,  k=0,1,2现在射击 $N$ 次，其中得 $0$ 分的有 $a_0$ 次，其中得 $1$ 分的有 $a_1$ 次，其中得 $2$ 分的有 $a_2$ 次，$a_0+a_1+a_2=N$。他射击$N$次得分的总和为$a_0\ast 0+a_1\ast 1+a_2\ast 2$。于是平均一次射击的得分为：$$\frac{a_0\ast 0+a_1\ast 1+a_2\ast 2}{N}=\sum _{k=0}^{2}k\frac{a_k}{N}$$这里，$\frac{a_k}{N}$是事件 { X = k } \{X=k\} {
X=k}，当$N$很大时，$\frac{a_k}{N}$在一定意义下接近于事件 { X = k } \{X=k\} {
X=k}的概率$p_k$。就是说，在实验次数很大时，随机变量$X$的观察值的平均数${\sum }_{k=0}^{2}k\frac{a_k}{N}$接近于${\sum }_{k=0}^{2}k{p}_k$，这一条就是大数定律的内容。我们称${\sum }_{k=0}^{2}k{p}_k$为随机变量$X$的数学期望。一般，有以下定义。

  定义   设离散随机变量$X$的分布律为 P { X = x k } = p k ,    k = 1 , 2 , ⋯   . P\{X=x_k\}=p_k,\ \ k=1,2,\cdots. P{
X=xk​}=pk​,  k=1,2,⋯.若级数$$\sum _{k=1}^{\infty }{x}_k{p}_k$$绝对收敛，则称级数${\sum }_{k=1}^{\infty }{x}_k{p}_k$的和为随机变量$X$的数学期望，记为$E(X)$。即$$E(X)=\sum _{k=1}^{\infty }{x}_k{p}_k$$  设连续型随机变量$X$的概率密度为$f(x)$，若积分$${\int }_{-\infty }^{\infty }f(x)dx$$绝对收敛，则称积分${\int }_{-\infty }^{\infty }f(x)dx$的值为随机变量$X$的数学期望，记为$E(X)$。即$$E(X)={\int }_{-\infty }^{\infty }f(x)dx$$  数学期望简称期望，又称均值。
  数学期望$E(X)$完全由随机变量$X$的概率分布所决定。若$X$服从某一分布，也称$E(X)$是这一分布的数学期望。

样本均值与总体均值差异：

（1）样本均值的计算依据是样本个数，总体均值的计算依据是总体的个数。一般情况下样本个数小于等于总体个数。
（2）样本均值代表着所抽取的样本的集中趋势，而总体均值代表着全体个体的集中趋势。样本来自总体，但是样本只是总体的一部分，一般有差异。
（3）选取样本的个数非常接近以至于等于总体的个数，那么样本均值与总体均值描述的就是一个对象了，这样二者自然就相等了，这一条就是大数定律的内容。

  下面是方差，方差是用来计算变量与均值之间的差异。如果这个均值采用的是总体均值$\mu$(数学期望)，则结果为总体方差 ${\sigma }^2=\frac{1}{N}{\sum }_{i=1}^N(X_i-\mu {)}^2$；但是，如果这个均值采用的是样本均值$\overline{X}$，样本方差$S^2=\frac{1}{N}{\sum }_{i=1}^N(X_i-\overline{X}{)}^2$，样本方差定义成这样是有偏差的，这不是真正的样本方差。为了纠正这个偏量，将 样本方差 定义为：$S^2=\frac{1}{N-1}{\sum }_{i=1}^N(X_i-\overline{X}{)}^2$，具体为什么样本方差除以$N-1$而不是$N$，下面最大似然求高斯分布估计量的时候会说明。在这里也可以看出，是跟均值有关系，由于样本均值与总体均值的不一致导致的偏差。

2 最大似然估计

  极大似然估计方法（Maximum Likelihood Estimate，MLE）也称为最大概似估计或最大似然估计，是求估计的另一种方法，最大概似是1821年首先由德国数学家高斯（C. F. Gauss）提出。

2.1 分布率与概率密度函数

  概率分布，是指用于表述随机变量取值的概率规律，即随机变量的可能取值及取得对应值的概率。对于离散性的随机变量的分布率记为 $p(x)$；连续型随机变量的概率密度函数记为 $f(x)$，本质上是一个东西，只是一个是离散的一个是连续的。以含有参数 $\theta$ 的分布率为例，形式上表示为：$p(x;\theta )=p(x,\theta )=p(x|\theta )$，在机器学习中，这些表示都是一个意思，都表示在含有参数 $\theta$ 的情况下，$x$ 的概率。

2.2 似然函数

  样本 $X_1,X_2,\dots ,X_N$ 取到观察值 $x_1,x_2,\dots ,x_N$ 的概率 $L(\theta )$，称为似然函数。

• 若总体 $X$ 为离散型，且分布律 $P(X=x)=p(x;\theta )$，则似然函数 $L(\theta )=P(X_1=x_1,X_2=x_2,\dots ,X_N=x_N,)={\prod }_{i=1}^{N}p(X_i=x_i)={\prod }_{i=1}^{N}p(x_i;\theta )$；
• 若总体 $X$ 为连续型，且概率密度函数为 $f(x)=f(x;\theta )$，由于$P(x=x_i)=0$，则考虑 $X$ 落在点 $x_i$ 的某一领域 $U(x_i)$ 内的概率，$P(X_1\in U(x_1)，X_2\in U(x_{1}2)，\dots ，X_N\in U(x_N))=f(x_1;\theta )d{x}_{1}f(x_2;\theta )d{x}_2\dots f(x_N;\theta )d{x}_N={\prod }_{i=1}^{N}f(x_i;\theta )$，取似然函数 $L(\theta )={\prod }_{i=1}^{N}f(x_i;\theta )$

2.3 最大似然的目的

  在位置参数 $\theta$ 的取值范围内求 $\hat{\theta }$，使$L(\hat{\theta })=maxL(\theta )$，即 $\theta$ 的最大似然估计 $\hat{\theta }$ 为似然估计 $L(\theta )$ 的最大值点。

2.4 最大似然求解步骤

第一步：写出似然函数 $L(\theta )$，并取对数 $log$，对数可以以 $2$ 为底也可以以 $e$为 底；
第二步：令 $\frac{dlogL(\theta )}{d\theta }=0$ 或 $\frac{\partial logL({\theta }_1,{\theta }_2)}{\partial {\theta }_i}=0(i=1,2)$，建立方程（组）。若从中解的唯一驻点 $\hat{\theta }=\hat{\theta }(X_1,X_2,\dots ,X_N)$ 或 $\hat{\theta }=({\hat{\theta }}_1,{\hat{\theta }}_2)=({\hat{\theta }}_1(X_1,X_2,\dots ,X_N),{\hat{\theta }}_2(X_1,X_2,\dots ,X_N))$，则 $\hat{\theta }$为$\theta$ 的最大似然估计；
第三步：若上述方程无解，则$L(\theta )$ 为 $\theta$ 或 ${\theta }_1,{\theta }_2$ 的单调函数，$\hat{\theta }$ 在端点或边界上取得，需要根据具体情况具体分析。

2.5 最大似然估计的不变性

  设 $\hat{\theta }$ 是未知参数 $\theta$ 的最大似然估计量，对于 $\theta$ 的函数 $g(\theta )$，如果 $g(\theta )$ 具有单值反函数，则 $g(\hat{\theta })$ 是 $g(\theta )$ 的最大似然估计量。例如，均值位置的正太总体 $N(\mu ,{\sigma }^2)$ 的方差 ${\sigma }^2$ 的最大似然估计量为 ${\hat{\sigma }}^2=\frac{1}{N}{\sum }_{i=1}^N(X_i-\overline{X}{)}^2$，则总体标准差 $\sigma$ 的最大似然估计为 $\sigma =\sqrt{\frac{1}{N}{\sum }_{i=1}^N(X_i-\overline{X}{)}^2}$。

2.6 最大似然估计量的评选标准

2.6.1 无偏性

  设 $\hat{\theta }$ 为 $\theta$ 的估计量，若$E(\hat{\theta })=\theta$，就称$\hat{\theta }$为$\theta$的无偏估计，否则称为有偏估计。若${\lim }_{N\to \infty }E(\hat{\theta })=\theta$，就称$\hat{\theta }$为$\theta$的渐近无偏估计。
  常用结论：

• $\overline{X}$是$E(X)=\mu$的无偏估计，即$E(\overline{X})=E(X)=\mu$；
• $S^2$是$D(X)={\sigma }^2$的无偏估计，即$E(S^2)=D(X)={\sigma }^2$；
• 设估计量${\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_N,$均为$\theta$的无偏估计量，$c_1,c_2,\cdots ,c_N$为常数，且${\sum }_{i=1}^N{c}_i=1$，则$c_1{\hat{\theta }}_1,c_2{\hat{\theta }}_2,\cdots ,c_N{\hat{\theta }}_N$仍为$\theta$的无偏估计。

【注】若$\hat{\theta }$为$\theta$的无偏估计，则$g(\hat{\theta })$未必是$g(\theta )$的无偏估计。

2.6.2 有效性

  设${\hat{\theta }}_1,{\hat{\theta }}_2$均为$\theta$的无偏估计，若$D({\hat{\theta }}_1)<D({\hat{\theta }}_2)$，就称${\hat{\theta }}_1$比${\hat{\theta }}_2$更有效。总之，期望相同比方差。

2.6.3 一致性(相合性)

  若对$\forall \epsilon >0$，有${\lim }_{N\to \infty }P\left\{|\hat{\theta }-\theta |<\epsilon \right\}=1$，就称$\hat{\theta }$为$\theta$的一致估计量或相合估计量。

3 一维高斯分布

3.1 一维高斯分布概率密度函数

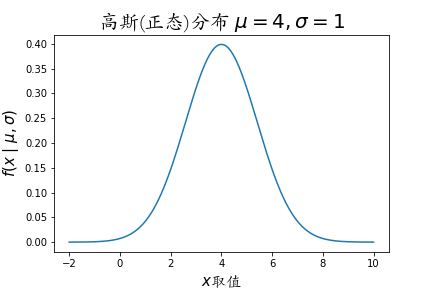
一维高斯分布(正态分布)函数：$$f(x|\mu ,\sigma )=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$ 或者这种写法 $$f(x|\mu ,\sigma )=\frac{1}{\sqrt{2\pi }\sigma }exp\left\{-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right\}$$
高斯分布图像，以 $\mu =4,\sigma =1$ 为例：

3.1 一维高斯分布最大似然估计以及检测估计量的无偏性

题目 ：设总体$X\sim N(\mu ,{\sigma }^2),(X_1,X_2,\cdots ,X_N)$为来自总体$X$的样本。
（1）如果${\sigma }^2$已知，$\mu$未知，求$\mu$的最大似然估计量$\hat{\mu }$。
（2）如果$\mu$已知，${\sigma }^2$未知，求${\sigma }^2$的最大似然估计量${\hat{\sigma }}^2$。
（3）如果$\mu$，${\sigma }^2$均未知，求$\mu$，${\sigma }^2$的最f大似然估计量$\hat{\mu }$，${\hat{\sigma }}^2$。

分析：
样本数据 $Data:$ $$X=\left(\begin{array}{c}{x}_1,x_2,\cdots ,x_N\end{array}\right)={\left(\begin{array}{c}{x}_1^p\\ x_2^p\\ ⋮\\ x_N^p\end{array}\right)}_{N\times p},x_i\in {\mathbb{R}}^p,x_i\stackrel{iid}{\sim }N(\mu ,{\sigma }^2)$$ 目标函数$Goal:$ 求最大似然估计。为了方便表示函数，用参数 $\theta$ 表示参数 $(\mu ,\sigma )$ $$MLE:\hat{\theta }=arg\underset{\theta }{\max }lnL(X|\mu ,\sigma )$$ 【注】因为高斯分布的概率密度中有以 $e$ 为底的指数函数，为了方便计算。所以这里的对数似然函数选取以 $e$ 为底的 $ln$。

解：
（1）设$x_1,x_2,\cdots ,x_N$为样本的观测值，由于${\sigma }^2$已知，$\mu$未知，似然函数为：$$\begin{array}{rl}L(X|\mu )& =\prod _{i=1}^{N}p(x_i|\mu )\\ & =\prod _{i=1}^N\frac{1}{\sqrt{2\pi }\sigma }exp\left\{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}\right\}\end{array}$$ 似然函数取对数： $$\begin{array}{rl}lnL(X|\mu )& =ln\prod _{i=1}^{N}p(x_i|\mu )\\ & =ln\prod _{i=1}^N\frac{1}{\sqrt{2\pi }\sigma }exp\left\{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}\right\}\\ & =-\frac{N}{2}ln(2\pi )-Nln\sigma -\frac{1}{2{\sigma }^2}\sum _{i=1}^N(x_i-\mu {)}^2\end{array}$$ 对数似然取导数：$$\frac{dlnL(X|\mu )}{d\mu }=\sum _{i=1}^N\frac{1}{{\sigma }^2}(x_i-\mu )=0$$ $$\sum _{i=1}^N(x_i-\mu )=0$$ $$\sum _{i=1}^N{x}_i-N\mu =0$$ $$\hat{\mu }=\frac{1}{N}\sum _{i=1}^N{X}_i=\overline{X}(发现结果为样本均值)$$ 从结果中可以看出，$\mu$的最大似然估计量，只受样本值的影响。从定义的角度证明：$$E[\hat{\mu }]=E[\frac{1}{N}\sum _{i=1}^N{X}_i]=\frac{1}{N}\sum _{i=1}^{N}E[X_i]=\frac{1}{N}N\mu =\mu$$即，$\hat{\mu }$为$\mu$的无偏估计量。

（2）设$x_1,x_2,\cdots ,x_N$为样本的观测值，由于$\mu$已知，${\sigma }^2$未知，似然函数为：$$\begin{array}{rl}L(X|{\sigma }^2)& =\prod _{i=1}^{N}p(x_i|{\sigma }^2)\\ & =\prod _{i=1}^N\frac{1}{\sqrt{2\pi }\sigma }exp\left\{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}\right\}\end{array}$$ 似然函数取对数： $$\begin{array}{rl}lnL(X|{\sigma }^2)& =ln\prod _{i=1}^{N}p(x_i|{\sigma }^2)\\ & =ln\prod _{i=1}^N\frac{1}{\sqrt{2\pi }\sigma }exp\left\{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}\right\}\\ & =-\frac{N}{2}ln(2\pi )-\frac{N}{2}ln({\sigma }^2)-\frac{1}{2{\sigma }^2}\sum _{i=1}^N(x_i-\mu {)}^2\end{array}$$ 对数似然取导数：$$\frac{dlnL(X|{\sigma }^2)}{d{\sigma }^2}=\sum _{i=1}^N\frac{1}{{\sigma }^2}(x_i-\mu )=0$$$$-\frac{N}{2{\sigma }^2}+\frac{1}{2{\sigma }^4}\sum _{i=1}^N(x_i-\mu {)}^2=0$$ $${\hat{\sigma }}^2=\frac{1}{N}\sum _{i=1}^N(X_i-\mu {)}^2$$ 从结果中可以看出，${\hat{\sigma }}^2$受到样本值以及均值$\mu$的影响，但是题目中已经说明，$\mu$是已知条件，所以这里的$\mu$就是已知的总体均值，所以本质上${\hat{\sigma }}^2$也仅受样本值的影响。从定义的角度证明： $$\begin{array}{rl}E[{\hat{\sigma }}^2]& =E[\frac{1}{N}\sum _{i=1}^N(X_i-\mu {)}^2]\\ & =E[\frac{1}{N}\sum _{i=1}^N{X}_i^2-\frac{1}{N}\sum _{i=1}^{N}2X_i\mu +\frac{1}{N}\sum _{i=1}^N{\mu }^2]\\ & =E[\frac{1}{N}\sum _{i=1}^N{X}_i^2-2{\mu }^2+{\mu }^2]\\ & =E[(\frac{1}{N}\sum _{i=1}^N{X}_i^2-{\mu }^2)]\\ & =\frac{1}{N}\sum _{i=1}^N(E(X_i^2)-E^2(X_i))\\ & =D(X_i)\\ & ={\sigma }^2\end{array}$$ 即${\hat{\sigma }}^2$为${\sigma }^2$的无偏估计。

（3）设$x_1,x_2,\cdots ,x_N$为样本的观值，$\mu$，${\sigma }^2$均未知，似然函数为：$$\begin{array}{rl}L(X|\mu ,{\sigma }^2)& =\prod _{i=1}^{N}p(x_i|\mu ,{\sigma }^2)\\ & =\prod _{i=1}^N\frac{1}{\sqrt{2\pi }\sigma }exp\left\{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}\right\}\end{array}$$ 似然函数取对数：$$\begin{array}{rl}lnL(X|\mu ,{\sigma }^2)& =ln\prod _{i=1}^{N}p(x_i|{\sigma }^2)\\ & =ln\prod _{i=1}^N\frac{1}{\sqrt{2\pi }\sigma }exp\left\{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}\right\}\\ & =-\frac{N}{2}ln(2\pi )-\frac{N}{2}ln({\sigma }^2)-\frac{1}{2{\sigma }^2}\sum _{i=1}^N(x_i-\mu {)}^2\end{array}$$ 分别对$\mu$与${\sigma }^2$取偏导：$$\frac{\partial lnL(X|\mu ,{\sigma }^2)}{\partial \mu }=\sum _{i=1}^N\frac{1}{{\sigma }^2}(x_i-\mu )=0$$ $$\sum _{i=1}^N(x_i-\mu )=0$$ $$\hat{\mu }=\frac{1}{N}\sum _{i=1}^N{X}_i=\overline{X}$$ $$\frac{\partial lnL(X|\mu ,{\sigma }^2)}{\partial {\sigma }^2}=-\frac{N}{2{\sigma }^2}+\frac{1}{2{\sigma }^4}\sum _{i=1}^N(x_i-\mu {)}^2=0$$ $$-N+\frac{1}{{\sigma }^2}\sum _{i=1}^N(x_i-\mu {)}^2=0$$ $${\hat{\sigma }}^2=\frac{1}{N}\sum _{i=1}^N(X_i-\hat{\mu }{)}^2=\frac{1}{N}\sum _{i=1}^N(X_i-\overline{X}{)}^2$$
在下面的无偏性检验中，可以发现$\hat{\mu }$为无偏性估计，而${\hat{\sigma }}^2$为有偏性估计。因为求高斯分布时，参数$\mu ,{\sigma }^2$都是未知的，而求$\hat{\mu }$时，不需要依赖未知参数${\sigma }^2$(计算时被约去了)；而计算${\hat{\sigma }}^2$时，需要依赖$\mu$，但是$\mu$也未知，所以只能用已计算出来的$\hat{\mu }$代替，而不是真正的总体均值$\mu$，这就是有偏的原因。根据定义证明：
（a）检测估计量$\hat{\mu }$的无偏性$$E[\hat{\mu }]=E[\overline{X}]=E[\frac{1}{N}\sum _{i=1}^N{X}_i]=\frac{1}{N}\sum _{i=1}^{N}E[X_i]=\frac{1}{N}N\mu =\mu$$ 即$\hat{\mu }$为$\mu$的无偏估计。
（b）检测估计量$\widehat{{\sigma }^2}$的无偏估计，且需要明确一些条件： $$估计量\hat{\mu }的方差：D(\hat{\mu })=D(\overline{X})=D(\frac{1}{N}\sum _{i=1}^N{X}_i)=\frac{1}{N^2}\sum _{i=1}^{N}D(X_i)=\frac{1}{N^2}N{\sigma }^2=\frac{{\sigma }^2}{N}$$ $$总体方差：D(X_i)={\sigma }^2=\frac{1}{N}\sum _{i=1}^N(X_i-\mu {)}^2$$ $$\begin{array}{rl}E[{\hat{\sigma }}^2]& =E[\frac{1}{N}\sum _{i=1}^N(X_i-\overline{X}{)}^2]\\ & =E[\frac{1}{N}\sum _{i=1}^N{X}_i^2-\frac{1}{N}\sum _{i=1}^{N}2X_i\overline{X}+\frac{1}{N}\sum _{i=1}^N{\overline{X}}^2]\\ & =E[\frac{1}{N}\sum _{i=1}^N{X}_i^2-2{\overline{X}}^2+{\overline{X}}^2]\\ & =E[(\frac{1}{N}\sum _{i=1}^N{X}_i^2-{\mu }^2)-({\overline{X}}^2-{\mu }^2)]\\ & =E[\frac{1}{N}\sum _{i=1}^N(X_i^2-{\mu }^2)]-E({\overline{X}}^2-{\mu }^2)\\ & =\frac{1}{N}\sum _{i=1}^N(E(X_i^2)-E^2(X_i))-(E({\overline{X}}^2)-E^2(\overline{X}))\\ & =D(X_i)-D(\overline{X})\\ & ={\sigma }^2-\frac{{\sigma }^2}{N}\\ & =\frac{N-1}{N}{\sigma }^2\end{array}$$ 显然，所求结果$E({\hat{\sigma }}^2)$不等于${\sigma }^2$，${\hat{\sigma }}^2$为有偏估计，既然有偏就需要纠偏，样本的方差该如何表示呢？根据结果，看出偏移的部分是系数$\frac{N-1}{N}$，那就在原方程的基础上乘以系数的倒数$\frac{N}{N-1}$，将系数部分抵消掉，这样结果就只剩${\sigma }^2$了，就是无偏估计了。则无偏的样本方差$S^2$定义为：$$S^2=\frac{N}{N-1}\frac{1}{N}\sum _{i=1}^N(X_i-\overline{X}{)}^2=\frac{1}{N-1}\sum _{i=1}^N(X_i-\overline{X}{)}^2=\frac{1}{N-1}\sum _{i=1}^N(X_i^2-N\overline{X})$$

参考：浙大版概率论与数理统计