统计|如何建立单总体方差的置信区间

大家好，欢迎来到IT知识分享网。

本博文源于《商务统计》，旨在研究单总体方差的区间估计的建立。总所周知根据大数定律来看，样本越大，越能较好的模拟总体样本分布。因此当我们已经了解了样本的方差时，是否能直接推出总体方差呢？

正态分布的可怕性

看见题目中出现服从正态分布一头雾水，正态分布到底能做什么？根据中心极限定理来讲，随着样本不断变大，样本就会必然服从正态分布。

正态分布推出卡方分布

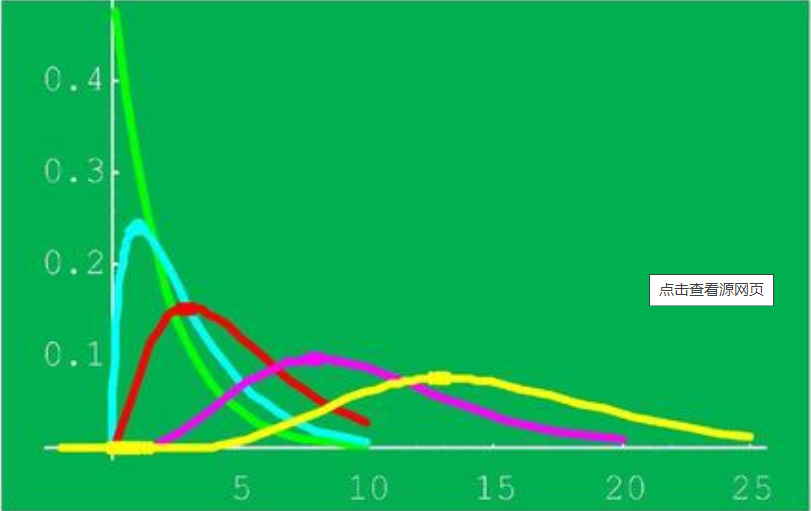
冷不丁的放出卡方分布干嘛，大家从图中看出，随着n增大，越来趋近于正态分布，不过有点平原的感觉，但卡方分布的定义中就是服从正态分布，因此，我们《统计学》中有这样一个公式去估计总体的方差：

然后推出(方差)：

标准差：

• n是样本大小
• αz置信水平一般1-α
• S是样本方差

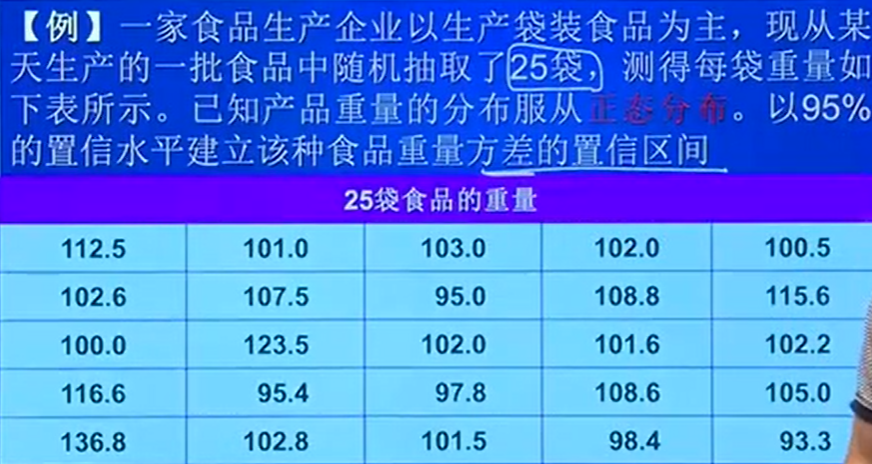
例子：食品质量检测

解题步骤

• n=25
• 1-α=95%
• 求取样本方差，s^2=93.21
• 查自由度25-1的卡方分布表
• 带入公式，计算结果，收获喜悦！

解题细节

总结

因为我们想知道总体方差，所以我们先要计算样本的方差，样本的方差知道后，根据卡方分布表查询，最后带入公式进行计算，测得最后的单总体方差的置信区间。