最后一次回顾KMeans聚类算法

大家好，欢迎来到IT知识分享网。

最后一次回顾KMeans聚类算法。

KMeans聚类算法的原理

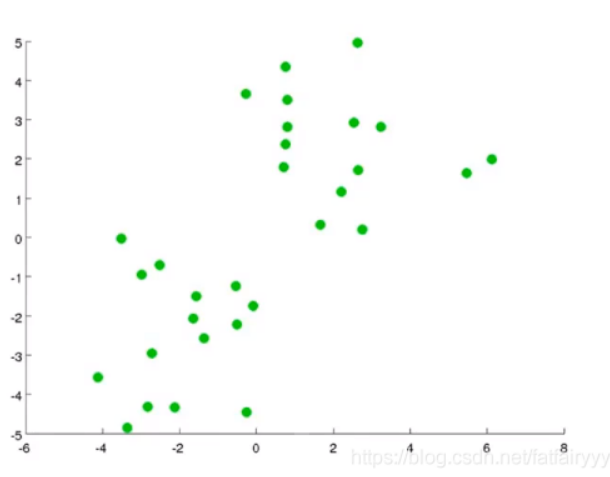
• 一个数据集如下，我们希望将它分为两个簇（因为通过人的观察，它看起来像是可以分成两个簇，KMeans聚类算法的K是需要操作人员自己选择的，这也是这个算法的弊端之一，可以通过肘部法则（手肘法）来改善）👇。
  
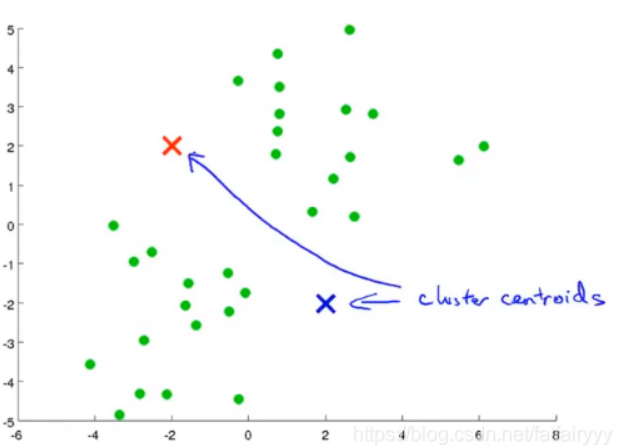
• KMeans聚类算法的第一步，是初始化聚类中心。通常我们使用随机初始化的方法，即，在已经给定的样本点中选取聚类中心。但此处为了说明问题，使用了另一种方法初始化聚类中心，但是无论使用哪种初始化的方法，最终都是有可能得到最佳结果的。
  
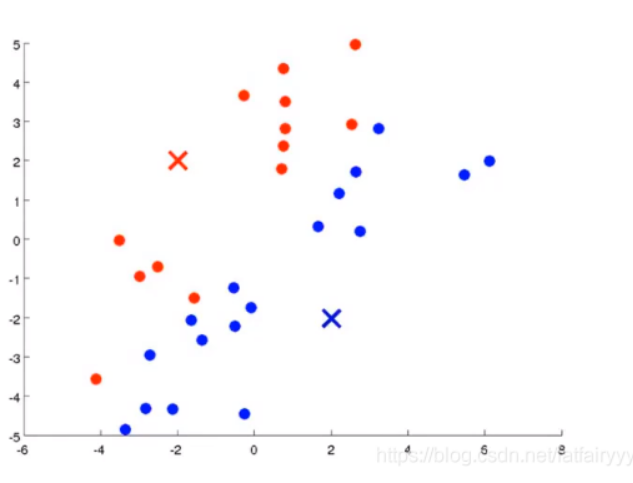
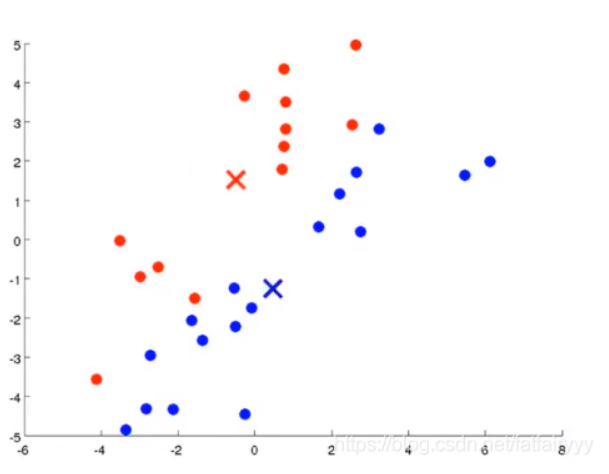
  👆生成两个聚类中心，因为我们希望将数据集分为两个簇。
• 显然，KMeans聚类算法是一个需要迭代的方法，它通过不断的迭代，改变聚类中心的位置和样本点与聚类中心的关系划分，当迭代不使结果产生改变时 ，说明分类的工作已经完成，可以退出循环返回结果了。每一步的迭代，KMeans聚类算法要做两件事，第一件事是为样本点寻找合适的聚类中心，即，某个样本点与哪一个聚类中心的欧氏距离最近，那么就将这个样本点划分给哪个聚类中心。
  
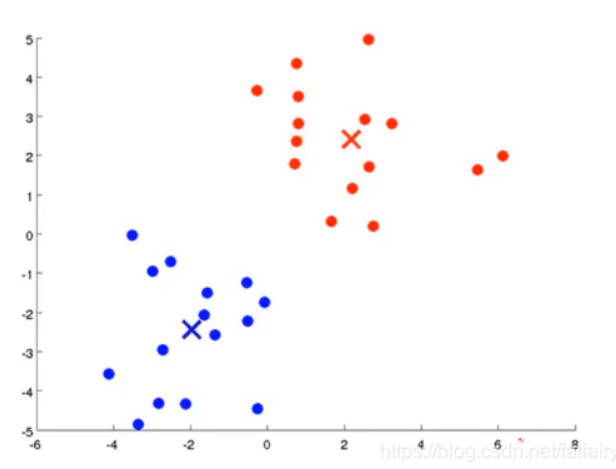
• KMeans聚类算法要做的另一件事情，是改变聚类中心，由上图可知，由于该例中只需要将数据集分为两个簇，因此使用红色和蓝色代表两个簇的聚类中心和簇中样本点。改变聚类中心，说的是将某个簇的聚类中心重新放到属于这个簇的样本点的平均中心位置。
  
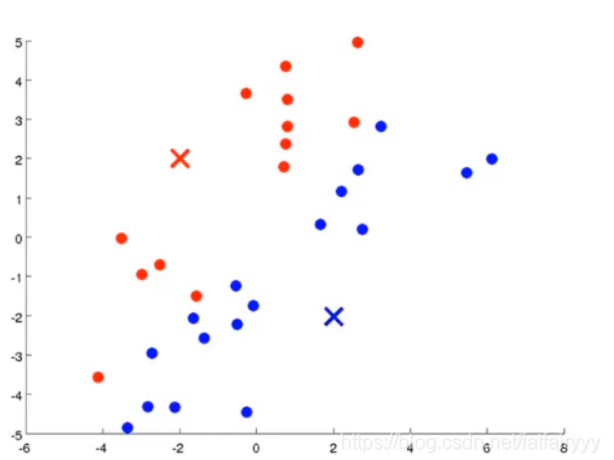
  👆聚类中心改变前，聚类中心改变后👇
  
  划分完聚类中心之后，便进入到了下一次迭代，此时要先重新为所有样本点选择新的聚类中心，因为上一次迭代的最后一步，聚类中心的位置改变了。之后再改变聚类中心的位置，依次迭代，直到聚类中心的位置和样本点的划分都不再发生改变，结束迭代，分类完成。
  

KMeans聚类算法的缺点

• 聚类的个数在开始就要设定。
• 聚类的结果取决于初始设定的聚类中心。
• 对异常值很敏感。
• 不适合用于发现非凸聚类问题。
• 不能保证得到全局最优解，它往往会陷入一个局部最优解。 此时重复运行算法是有可能得到全局最优解的。

KMeans聚类算法的Python实现

import numpy as np
import matplotlib.pyplot as plt
import random
from sklearn.datasets import make_blobs
np.random.seed(123)

# 从自带的机器学习库中获取数据，转移到变量中
X,y = make_blobs(centers=4,n_samples=1000) #四个聚类中心，1000个样本点
print(f'Shape of dataset:{X.shape}')# 打印数据集的大小
fig = plt.figure(figsize=(8,6))#准备绘制簇图像
plt.scatter(X[:,0],X[:,1],c = y)#X[:,0]代表取所有行中的第0个数据，即第0列数据
#👆数据集X的维度是(1000,2)的。
plt.title("Dataset with 4 clusters")#手动选择聚类中心，此处选择为4
#👆通过肘部法则可以选择聚类中心
plt.xlabel("First feature")
plt.ylabel("Second feature")
plt.show()
#👆展示初始数据集

#👇KMeans聚类算法：
class KMeans():
    def __init__(self,n_clusters = 4):
        self.k = n_clusters #初始化K为聚类中心个数

    def fit(self,data):#训练KMeans聚类算法模型
        """ 取数据集当中的一小部分用来训练K-Means聚类算法模型 """
        n_samples,_ = data.shape #样本量为数据集的大小。
        #👇初始化聚类中心
        self.centers = np.array(random.sample(list(data),self.k)) #随机初始化聚类中心，个数为4
        self.initial_centers = np.copy(self.centers) #随机初始化
        #继续追踪样本点到聚类中心的欧氏距离是否改变，如果不再改变，停止迭代，分类完成
        #停止迭代的条件是，每一个样本点被分配到的聚类中心不再改变，重点在于每一个样本点
        old_assigns = None
        n_iters = 0 #记录迭代次数

        while True: #永真循环，因为结束迭代的条件是聚类中心位置和样本点的聚类划分不再改变。
            new_assigns = [self.classify(datapoint) for datapoint in data]
            #👆对于本例，有1000个数据，因为有1000个样本点
            #👆为所有样本点重新划分新的聚类中心。
            if new_assigns == old_assigns: #如果划分没有改变，那么就代表聚类中心的位置没有改变
            #如果这两条都满足，那么就说明划分完成，实际上，只要一条满足，就代表划分完成。
                print(f"Training finished after {n_iters} iterations!")
                return

            old_assigns = new_assigns
            n_iters += 1

            #根据欧氏距离重新计算聚类中心
            for id_ in range(self.k): #重新部署聚类中心的位置。
                points_idx = np.where(np.array(new_assigns) == id_)
                datapoints = data[points_idx]
                self.centers[id_] = datapoints.mean(axis = 0)
    def l2_distance(self,datapoint):#计算欧氏距离
        dists = np.sqrt(np.sum((self.centers - datapoint)**2,axis=1))
        return dists

    def classify(self,datapoint):#为样本点分配它们的聚类中心
        """ Given a datapoint, compute the cluster closest to the datapoint. Return the cluster ID of that cluster. """
        dists = self.l2_distance(datapoint)
        return np.argmin(dists)#为许许多多的样本点重新分配聚类中心

    def plot_clusters(self,data):
        plt.figure(figsize=(12,10))
        plt.title("Initial centers in black,final centers in red")
        plt.scatter(data[:,0],data[:,1],marker = '.',c=y)
        plt.scatter(self.centers[:,0],self.centers[:,1],c='r')
        plt.scatter(self.initial_centers[:,0],self.initial_centers[:,1],c='k')
        plt.show()

if __name__ == '__main__':
    kmeans = KMeans(n_clusters = 4)
    kmeans.fit(X)
    kmeans.plot_clusters(X)

总结

总的来说，KMeans聚类算法是一个相当入门的用于分类的无监督学习算法，本文使用Python实现，更是简化了KMeans聚类算法的难度（Python算是描述性语言）。本文使用了Python自带的机器学习库sklearn，使用的样本也是来自sklearn库中的样本。