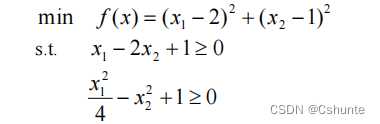Matlab遗传算法「终于解决」

大家好，欢迎来到IT知识分享网。

     遗传算法（Genetic Algorithm，GA）最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。

选择操作：

  从旧个体中以一定概率选择优良个体组成新的种群，以繁殖得到下一代

交叉操作：

  从种群中随机选择两个个体，通过两个染色体的交换组合，把父串的优秀特征遗传给子串，从而产生新的优秀个体

变异操作：

  从种群中随机选择一个个体，选择个体中的一点进行变异以产生更优秀的个体

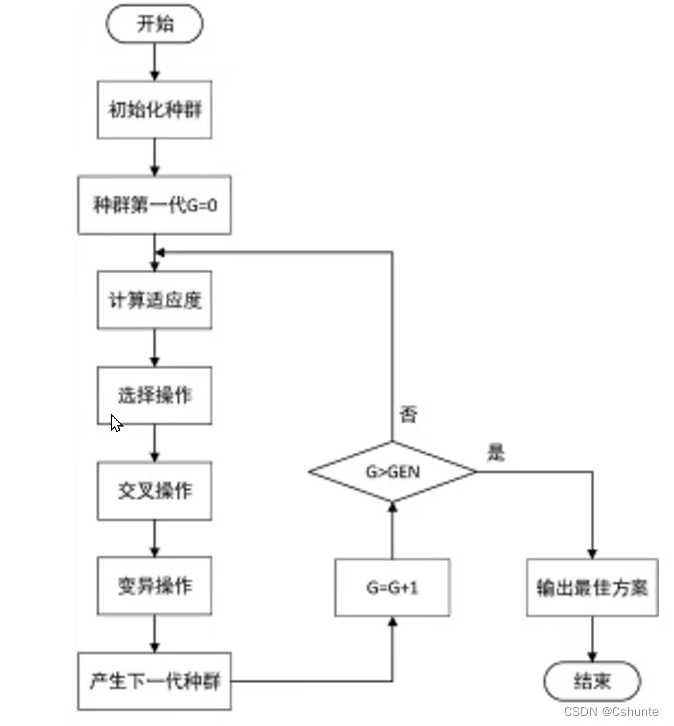
原理图：

Matlab中关于遗传算法自带的两个函数：gaoptimset()、ga()

gaoptimset()      设置遗传算法的一些参数

调用格式

options = gaoptimset('Param1', value1, 'Param2', value2, ...);（返回一个结构体）

Param1、Param2等是需要设定的参数，比如种群规模、交叉比例等等
value则是Param对应的值
CrossoverFraction             交叉比例                                                           0.8
Generations             算法中止的最大迭代次数                                           100
PopulationSize                 种群规模                                                             20
MigrationFraction             变异概率                                                             0.2
FitnessLimit       当适应度函数达到设定的值时算法中止                               –
StallGenLimit     当超过StallGenLimit代适应度函数为改善时，算法中止    50

ga()          %开始遗传算法的计算           （参数不需要则设置为空矩阵[]）

调用格式

[x_best,fval] = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options);

fun为目标函数句柄  （在定义的函数名前加个@即可）
nvars为自变量个数
A、b、Aeq、beq、lb、ub你都很熟了
nonlcon非线性约束函数句柄
options上述函数返回的结构体

举个栗子：

非线性约束函数的设立：

function [c,ceq] = nonlconfun(x)
c = -(1/4).*x(1)^2 + x(2)^2 - 1;
ceq = [];
end

目标函数句柄的设立：

function y = fun(x)
y = (x(1)-2)^2+(x(2)-1)^2;
end

主要m文件：

clc;clear
options = gaoptimset('PopulationSize', 300, 'Generations', 800);
nvars = 2;  A = [-1, 2];  b = [1];
Aeq = []; beq = []; lb = []; ub = [];
nonlcon = @nonlconfun; 
[x_best,fval] = ga(@fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options)

运行m文件，即可得到如下所示结果：

即当x1取2，x2取1的时候，函数取得最小值0