大家好，欢迎来到IT知识分享网。

【数据结构】排序——外部排序

外部排序是指大文件的排序，即排序的记录存储在外存储器上，在排序过程中需进行多次的内、外存之间的交换。

外部排序方法

通常采用归并排序

有外部排序基本上由两个相对独立的阶段组成。
按可用内存大小，将外存上含有n个记录的文件分成若干长度为l的字文件或段。
依次读入内存并利用有效的内部排序方法排序，将排序后得到的有序子文件（称为归并段或顺串），进行逐趟归并，直至得到整个有序文件为止。
在外部排序中实现两两归并，由于不可能将两个有序段及归并结果段同时存放在内存中的缘故，所以不仅要调用归并过程，还需要进行外存的读_写（对外存上信息的读_写是以“物理块”为单位的）。

耗费时间

总时间=内部排序时间(产生初始归并段)+外存读写时间+内部归并时间

内部排序时间=经过内部排序后得到的初始归并段的个数r * 得到一个初始归并段进行内部排序多需时间的均值
外存读写时间=总的读写次数 * 进行一次外存读写时间的均值
内部归并时间=归并的趟数s * n个记录进行内部归并排序的时间

优化方法

1. 增大归并路数k
2. 减少初始归并段个数r
   以上两个方法都可以减少归并的趟数，进而减少读写磁盘的次数，提高外部排序速度

多路平衡归并与败者树

已知增加k可以减少s，从而减少总的读写次数。如果只单纯的增加k又会导致内部归并时间增加。为了使内部归并不受k的增大而影响，提出了败者树。

败者树的基本思想

败者树是树形选择排序的一种变型，可视为一棵完全二叉树。
k个叶子节点分别存放k个归并段在归并过程中当前参加比较的记录，内部节点用来记忆左右子树中的“失败者”，而让胜者往上继续进行比较，一直到根结点。
若比较两个数，大的为败者、小的为胜利者，则根结点指向的数为最小数。
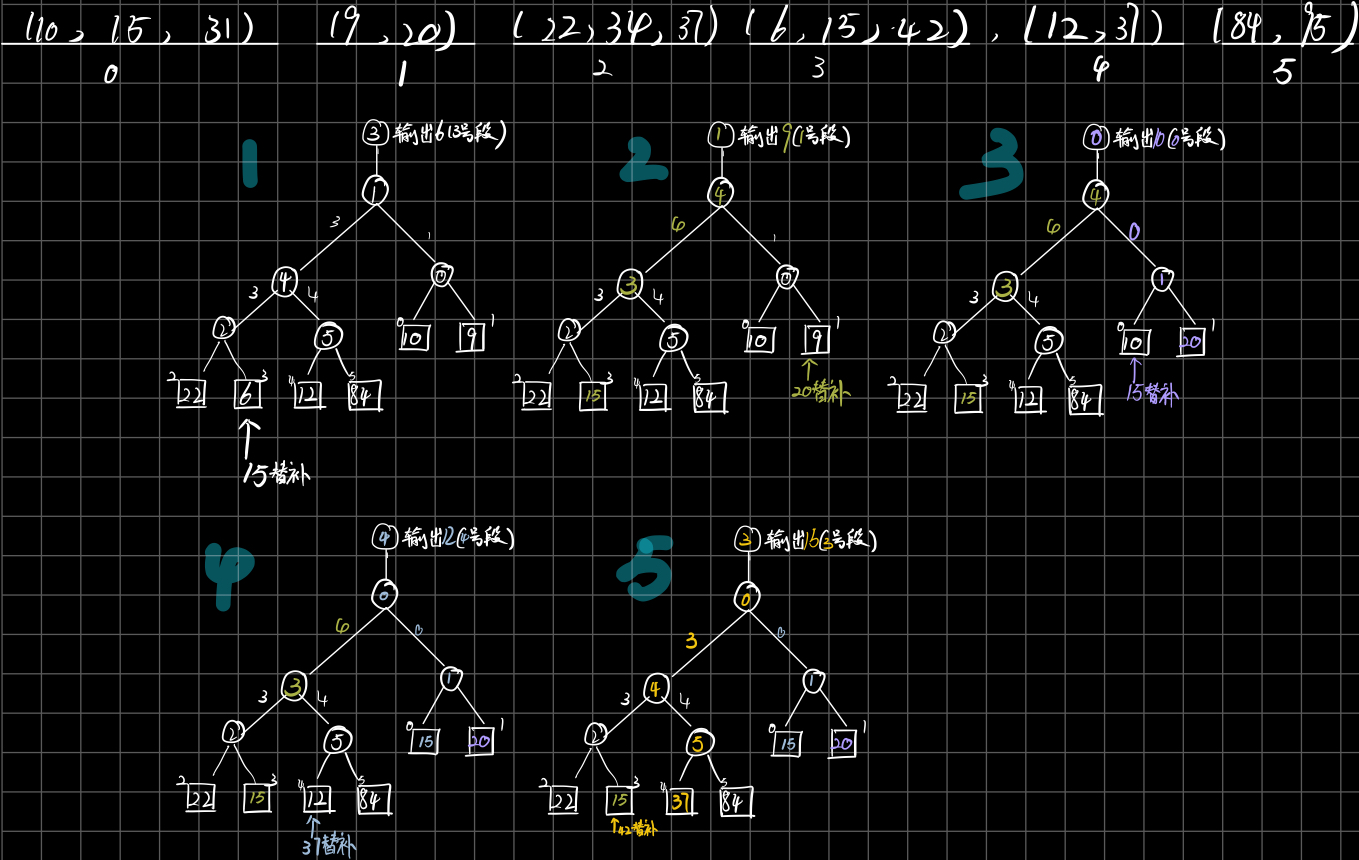
eg、设初始归并段为(10,15,31),(9,20),(6,15,42),(12,37),(84,95),利用败者树进行m路归并，手工执行选择最小的5个关键字的过程。

性能分析

k-路归并的败者树的深度为[log2k]+1

注意

⚠️在多路平衡归并中采用简单比较时，k越大，关键字的比较次数会越大。
⚠️在多路平衡归并中采用败者树时，关键字的比较次数与k无关，所以k越大越好。

优化

• 增加归并路数k，进行多路平衡归并
  代价1.需要增加相应的输入缓冲区。
  代价2.每次从k个归并段中选最小元素需要（k-1）关键字对比。
• 减少初始归并段数量r。

之前说到减少初始归并段数量或者是增大归并路数，都可以减少归并的趟数，进而减少磁盘的读写次数。

置换选择排序（生成初始归并段）

置换选择排序算法作用是由一个无序文件产生若干有序子文件。
用于生成初始归并段，通常产生的初始归并段个数较少
是在树形选择排序的基础上得来的的，特点是在整个排序的过程中，选择最小（或最大）关键字和输入、输出交叉或平行。

实现过程

FI：初始待排文件。FO：初始归并段输出文件。WA：内存工作区。FO和WA初始状态为空，WA可容纳w个记录

1. 从FI输入w个记录到工作区WA
2. 从WA中选出其中关键字取最小值得记录，极为MINMAX记录
3. 将MINMAX记录输出到FO中去
4. 若FI不为空，则从FI输入下一个记录到WA中
5. 从WA中所有关键字必MINMAX记录的关键字大的记录中选出最小关键字记录，作为新的MINMAX记录
6. 重复3-5，直至WA中选不出新的MINMAX记录为止，由此得到一个初始归并段，输出一个归并段的结束标志到FO中去
7. 重复2-6，直至WA为空，由此得到全部初始归并段。

手动实现过程

eg、FI={17、21、05、44、10、12、56、32、29}，WA=3。

其中WA区域中MINMAX记录选择是利用败者树完成。

最佳归并树（记录读写最少的归并方案）

由置换选择生成树所得初始归并段，其各长短不等对平衡归并有什么影响？
若将初始归并段的长度看成是归并树中叶子结点的权，显然，归并方案不同，所得归并树也不同，树的带权路径长度（或外存读写次数）也不同。因此若对长度不同的多个初始归并段，构造一棵哈夫曼树作为归并树，便可以使在进行外部归并时所需对外存进行的读写次数达到最少，这棵归并树成为最佳归并树。

结构概述

各叶结点表示一个初始归并段，上面的权值表示该归并段的长度；叶结点到根的路径长度表示其参加归并的趟数；各非叶结点代表归并成的新归并段；根结点表示最终生成的归并段；树的带权路径长度WPL为归并过程中的总读记录数。

算法优化

引入哈夫曼树的思想，在归并树中，让记录少的初始归并段最先归并，记录数多的初始归并段最晚归并，就可以建立总的读写次数最少的最佳归并树。
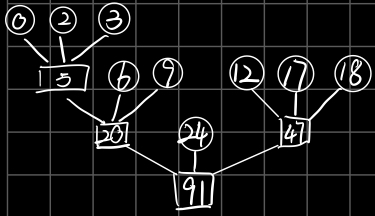
eg、由置换选择排序得到的9个初始归并段，其长度依次为{9,30,12,18,3,17,2,6,24}，现作3-路平衡归并

显然这不是最佳方案。

算法修正

若初始归并段不足以构成一棵严格k叉树时，则需要添加长度为0的“虚段”
按照哈夫曼树的原则，权为0的叶子应该离树根最远。

需要修正的条件

度为0的结点有n个，度为k的结点有m个。
严格k叉树有n=(k-1)m+1=>m=(n-1)/(k-1)
若(n-1)MOD(k-1)=0，则说明正好可以构造k叉归并树
若m=(n-1)MOD(k-1)=u（u不为0），则再加上k-u-1个空归并段就可以建立归并树。
eg、对于98个长度不等的初始归并段，在构建5路最佳归并树时需要增加多少个虚段？
解：k=5，n=98，k-(n-1)mod(k-1)-1 = 3,需要增加三个虚段。