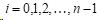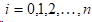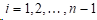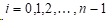大家好，欢迎来到IT知识分享网。
0 引 言
三次样条插值以构造简单，使用方便，拟合准确，具有“保凸”的重要性质等特点成为了常用的插值方法。一般三次样条插值解算过程中通过追赶法求解三弯矩阵，但使用计算机求解时会表现出解的精度不高的问题，导致其计算结果无法应用到工程实践之中。因此需要找出一种提高解精度的方法。
1 基本概念
三次样条函数的定义：在区间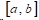
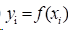
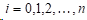
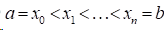
内对于给定的函数值 ，其中，如果函数满足条件：
（1） 
在每个子区间，上都是不高于三次的多项式；
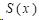
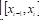
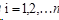
（2） 
、、在上都连续；
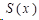
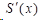
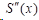
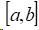
（3） 
， 。
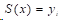
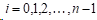
则称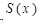
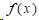
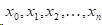
为函数关于节点的三次样条函数。
想要求解三次样条插值函数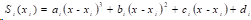
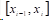
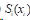
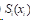
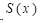
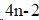
，只需在每个子区间上确定一个三次多项式共有4个系数，确定它们需要 4n 个条件，因此要完全确定共需 4n 个条件。由所满足的条件 （1）、（2）、（3），可确定个条件，仍然缺少两个条件。这两个条件通常由实际问题对三次样条插值函数在端点的状态要求给出，也称之为边界条件，常见的边界条件有：
1）夹持边界条件（Clamped Spline）：给定两端点的一阶导数值，即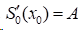
，；
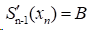
2）自然边界条件（Natural Spline）：使两端点的二阶导数值为零，即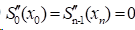
；
3）非扭结边界条件（Not-A-Knot Spline）：强制第一个插值点的三阶导数值等于第二个点的三阶导数值，最后第一个点的三阶导数值等于最后第二个点的三阶导数值，即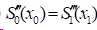
，。
2 计算方法
设三次样条函数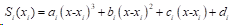
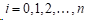
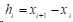
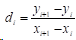
，（0）
，，
，
由三次样条函数定义（1）（2）（3）可得：
， （1）
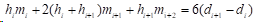
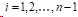
如下构造式（1）矩阵：
（2）
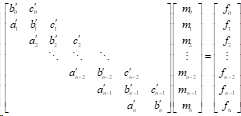
由式（1）可知：
，，，，
（3）
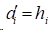
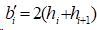
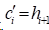
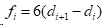
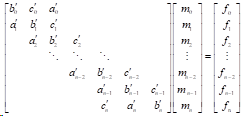
1）在夹持边界条件时，
，，，；
，，，；
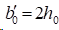
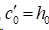
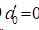
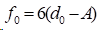
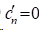
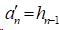
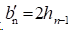
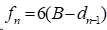
2）在自然边界条件时，
， ，，；
，，，；
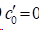
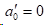
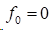
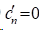
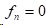
3）在非扭结边界条件时，
，，，；
，，，；
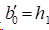
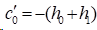
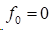
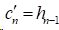
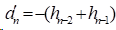
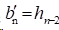
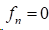
由n个未知数的非齐次方程组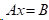
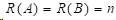
有惟一解的充分必要条件是，可知矩阵方程（2）在以上三种情况下都有惟一解。
对矩阵方程（2）采用高斯列主元消去法即可求解得出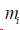
。
最后，代入式（0）可以得出：
，，，，
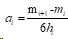
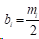
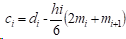
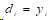
3 应用算例
有点集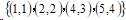
，在非扭结边界条件下进行插值。同时使用Matlab R2010a和文章所述方法进行插值计算，对比计算结果。
表1.Matlab R2010a计算结果
|
插值 方程 |
方程系数 |
|||
| a | b | c | d | |
|
0.083 333 333 333 333 2 |
-0.5 |
1.416 666 666 666 67 |
1 |
|
|
0.083 333 333 333 333 3 |
-0.25 |
0.666 666 666 666 667 |
2 |
|
|
0.083 333 333 333 333 3 |
0.25 |
0.666 666 666 666 667 |
3 |
|
表2.文章所述方法计算结果
|
插值 方程 |
方程系数 |
|||
| a | b | c | d | |
|
0.083 333 333 333 333 3 |
-0.5 |
1.416 666 666 666 665 |
1 |
|
|
0.083 333 333 333 333 3 |
-0.25 |
0.666 666 666 666 666 |
2 |
|
|
0.083 333 333 333 333 3 |
0.25 |
0.666 666 666 666 667 |
3 |
|
由表1、表2可知文章所述方法计算结果与Matlab R2010a计算一致，其他几种边界条件下的插值结论均一致，这里不在复述。
4 结 论
利用上述方法在传统的三弯矩阵中增加两个新元素，使得三次样条插值的求解过程可以在不增加计算复杂度的前提下提高计算结果精度。并且可以实现使用一种算法来计算三种常用边界条件下的样条插值函数。这样利于编制计算机程序来自动求解多种不同边界的三次样条函数。
1 /********************************************************** 2 ** 三次样条插值函数.C 3 ** 进行自然边界，夹持边界，非扭结边界条件下的插值 4 ** 5 ** 2012-05-25 将函数从原来的需要至少4个插值点才能计算 6 ** 扩展成只需要2个插值点就可以完成计算 7 ** 其他一些改变 8 ** 2008-12-27 创建函数 9 **********************************************************/ 10 #include <stdio.h> 11 #include <stdlib.h> 12 13 #define ABS(p) ( ((p) > 0) ? (p) : -(p) ) 14 #define SWAP(x, y, temp) (temp) = (y); (y) = (x); (x) = (temp); 15 16 typedef enum _condition 17 { 18 NATURAL, // 自然边界 19 CLAMPED, // 夹持边界 20 NOTAKNOT // 非扭结边界 21 }condition; 22 23 typedef struct _coefficient 24 { 25 double a3; 26 double b2; 27 double c1; 28 double d0; 29 }coefficient; 30 31 typedef struct _point 32 { 33 coefficient *coe; // 插值结果系数矩阵 34 double *xCoordinate; // 插值点横坐标 35 double *yCoordinate; // 插值点纵坐标 36 double f0; // 在夹持条件下的最左边点的导数值 37 double fn; // 在夹持条件下的最右边点的导数值 38 int num; // 插值点数 39 condition con; // 边界条件 40 }point; 41 42 43 /* 44 ** 资源不足时函数返回 -1 45 ** 插值点数小于2时，函数返回 -2 46 ** 计算正确完成函数返回插值点的数量 n 47 */ 48 int spline(point *point) 49 { 50 double *x = (*point).xCoordinate, *y = (*point).yCoordinate; 51 int n = (*point).num - 1; // 循环上限 52 int i; // 循环辅助变量 53 coefficient *coe = (*point).coe; 54 condition con = (*point).con; 55 double *h, *d; 56 double *a, *b, *c, *f, *m; 57 double temp; 58 59 if (n < 1) 60 {return -2;} 61 62 h = (double *)malloc( (6 * n + 4) * sizeof(double) ); /* 0, 1,...,(n-1) */ 63 if (h == NULL) 64 {return -1;} 65 d = h + n; /* 0, 1,...,(n-1) */ 66 a = d + n; /* 特别使用,1,...,(n-1), n */ 67 b = a + (n + 1); /* 0,1,...,(n-1), n */ 68 c = b + (n + 1); /* 0,1,...,(n-1),特别使用 */ 69 f = c + (n + 1); /* 0,1,...,(n-1), n */ 70 m = b; 71 72 73 /* 计算 h[] d[] */ 74 for (i = 0; i < n; i++) 75 { 76 h[i] = x[i + 1] - x[i]; 77 d[i] = (y[i + 1] - y[i]) / h[i]; 78 /* printf("%f\t%f\n", h[i], d[i]); */ 79 } 80 /********************** 81 ** 初始化系数增广矩阵 82 **********************/ 83 a[0] = (*point).f0; 84 c[n] = (*point).fn; 85 /* 计算 a[] b[] c[] f[] */ 86 switch(con) 87 { 88 case NATURAL: 89 f[0] = 0; 90 f[n] = 0; 91 a[0] = 0; 92 c[n] = 0; 93 c[0] = 0; 94 a[n] = 0; 95 b[0] = 1; 96 b[n] = 1; 97 break; 98 99 case CLAMPED: 100 f[0] = 6 * (d[0] - a[0]); 101 f[n] = 6 * (c[n] - d[n - 1]); 102 a[0] = 0; 103 c[n] = 0; 104 c[0] = h[0]; 105 a[n] = h[n - 1]; 106 b[0] = 2 * h[0]; 107 b[n] = 2 * h[n - 1]; 108 break; 109 110 case NOTAKNOT: 111 f[0] = 0; 112 f[n] = 0; 113 a[0] = h[0]; 114 c[n] = h[n - 1]; 115 c[0] = -(h[0] + h[1]); 116 a[n] = -(h[n - 2] + h[n - 1]); 117 b[0] = h[1]; 118 b[n] = h[n - 2]; 119 break; 120 } 121 122 for (i = 1; i < n; i++) 123 { 124 a[i] = h[i - 1]; 125 b[i] = 2 * (h[i - 1] + h[i]); 126 c[i] = h[i]; 127 f[i] = 6 * (d[i] - d[i - 1]); 128 } 129 /* for (i = 0; i < n+1; i++) printf("%f\n", c[i]); */ 130 131 /************* 132 ** 高斯消元 133 *************/ 134 if (n > 2) 135 { 136 /* 第0行到第(n-3)行的消元 */ 137 for(i = 0; i <= n - 3; i++) 138 { 139 /* 选主元 */ 140 if ( ABS(a[i + 1]) > ABS(b[i]) ) 141 { 142 SWAP(a[i + 1], b[i], temp); 143 SWAP(b[i + 1], c[i], temp); 144 SWAP(c[i + 1], a[i], temp); 145 SWAP(f[i + 1], f[i], temp); 146 } 147 temp = a[i + 1] / b[i]; 148 a[i + 1] = 0; 149 b[i + 1] = b[i + 1] - temp * c[i]; 150 c[i + 1] = c[i + 1] - temp * a[i]; 151 f[i + 1] = f[i + 1] - temp * f[i]; 152 } 153 } 154 if (n >= 2) 155 { 156 /* 最后3行的消元 */ 157 /* 第(n-2)行的消元 */ 158 /* 选主元 */ 159 if ( ABS(a[n - 1]) > ABS(b[n - 2]) ) 160 { 161 SWAP(a[n - 1], b[n - 2], temp); 162 SWAP(b[n - 1], c[n - 2], temp); 163 SWAP(c[n - 1], a[n - 2], temp); 164 SWAP(f[n - 1], f[n - 2], temp); 165 } 166 /* 选主元 */ 167 if ( ABS(c[n]) > ABS(b[n - 2]) ) 168 { 169 SWAP(c[n], b[n - 2], temp); 170 SWAP(a[n], c[n - 2], temp); 171 SWAP(b[n], a[n - 2], temp); 172 SWAP(f[n], f[n - 2], temp); 173 } 174 /* 消元 */ 175 temp = a[n - 1] / b[n - 2]; 176 a[n - 1] = 0; 177 b[n - 1] = b[n - 1] - temp * c[n - 2]; 178 c[n - 1] = c[n - 1] - temp * a[n - 2]; 179 f[n - 1] = f[n - 1] - temp * f[n - 2]; 180 /* 消元 */ 181 temp = c[n] / b[n - 2]; 182 c[n] = 0; 183 a[n] = a[n] - temp * c[n - 2]; 184 b[n] = b[n] - temp * a[n - 2]; 185 f[n] = f[n] - temp * f[n - 2]; 186 } 187 /* 最后2行的消元 */ 188 /* 第(n-1)行的消元 */ 189 /* 选主元 */ 190 if ( ABS(a[n]) > ABS(b[n - 1]) ) 191 { 192 SWAP(a[n], b[n - 1], temp); 193 SWAP(b[n], c[n - 1], temp); 194 SWAP(f[n], f[n - 1], temp); 195 } 196 /* 消元 */ 197 temp = a[n] / b[n-1]; 198 a[n] = 0; 199 b[n] = b[n] - temp * c[n - 1]; 200 f[n] = f[n] - temp * f[n - 1]; 201 202 /****************** 203 ** 回代求解 m[] 204 ******************/ 205 m[n] = f[n] / b[n]; 206 m[n - 1] = (f[n - 1] - c[n - 1] * m[n]) / b[n-1]; 207 for (i = n - 2; i >= 0; i--) 208 { 209 m[i] = ( f[i] - (m[i + 2] * a[i] + m[i + 1] * c[i]) ) / b[i]; 210 } 211 /* for (i = 0; i < n+1; i++) printf("%f\n", m[i]); */ 212 213 /*********************** 214 ** 计算插值函数所有参数 215 ***********************/ 216 for (i = 0; i < n; i++) 217 { 218 coe[i].a3 = (m[i + 1] - m[i]) / (6 * h[i]); 219 coe[i].b2 = m[i] / 2; 220 coe[i].c1 = d[i] - (h[i] / 6) * (2 * m[i] + m[i + 1]); 221 coe[i].d0 = y[i]; 222 } 223 free(h); 224 // 计算正确完成返回插值点的数量 225 return n + 1; 226 } 227 228 229 void main() 230 { 231 /* x[]内不能出现重复数据 */ 232 double x[] = { 0, 0.5, 0.75, 1.25, 2.5, 5, 7.5, 10, 15, 233 20, 25, 30, 35, 40, 45, 50, 55, 60, 234 65, 70, 75, 80, 85, 90, 95, 100}; 235 double y[] = { 0, 0.6107, 0.7424, 0.9470, 1.3074, 1.7773, 2.1, 236 2.3414, 2.6726, 2.8688, 2.9706, 3.0009, 2.9743, 2.9015, 237 2.7904, 2.6470, 2.4762, 2.2817, 2.0662, 1.8320, 1.5802, 238 1.3116, 1.0263, 0.7239, 0.4033, 0.0630}; 239 int n = sizeof(x) / sizeof(double); 240 coefficient *coe; 241 int i; 242 point p; 243 coe = (coefficient *)malloc((n - 1) * sizeof(coefficient)); 244 p.xCoordinate = x; 245 p.yCoordinate = y; 246 /* 下面两个参数f0和fn只在夹持条件下有效，其他条件下这两个值会被忽略 */ 247 p.f0 = 0;// 在夹持条件下的左边点的导数值 248 p.fn = 0;// 在夹持条件下的右边点的导数值 249 p.num = n; 250 p.con = NOTAKNOT; 251 p.coe = coe; 252 spline(&p); 253 254 for (i = 0; i < n - 1; i++) 255 printf("%f\t%f\t%f\t%f\n", coe[i].a3, coe[i].b2, coe[i].c1, coe[i].d0); 256 free(coe); 257 }
[参 考 文 献]
[1] 李桂成．计算方法[M] 北京：电子工业出版社，2006.8
[2] 司守奎、孙玺菁．数学建模算法与应用[M] 北京：国防工业出版社，2011.8
[3] 同济大学数学系．线性代数[M] 北京：高等教育出版社，2007.5
[4] 于洋 袁健华 钱江 王美玲．新边界条件下的三次样条插值函数[J]．软件 ，2016, (2)
[5] 何丽丽．三次样条插值–三转角方程的算法设计[J]．湖南邮电职业技术学院学报 ，2014, (3)
[6] 俞海军 陈瑾怡．三种插值方法的研究与比较[J]．河南科技 ，2013, (20)
[7] 乃明 胡兵 闵心畅．R-B方程样条有限元法[J]．四川大学学报（自然科学版） ，2012, 49(5)
[8] 邢丽．三次样条插值端点约束条件的构造与Matlab实现[J]．上海第二工业大学学报 ，2012, (4)
[9] 朱家明．两种三次样条插值建立方法及MATLAB运行时间比较[J]．中国培训，2016, (10)
[10] 张雨浓 劳稳超 肖林 陈宇曦．三次样条构造的伪逆解法[J]．计算机应用研究 ，2014, (2)
如果你觉得这个软件对你有用还可以打赏，打赏用户将会列入打赏榜单。也接受定制服务。
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://yundeesoft.com/30289.html
