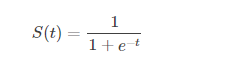Sigmoid函数总结

大家好，欢迎来到IT知识分享网。

Sigmoid函数又叫Logistic函数，它在机器学习领域有极其重要的地位。

目录
一 函数基本性质
二 Sigmoid函数与逻辑回归
三 为什么要选择Sigmoid函数
LR的需求选择Sigmoid是可以的
Sigmoid特殊的性质为什么选择Sigmoid
正态分布解释
最大熵解释
四 总结

一、 函数基本性质
首先Sigmoid的公式形式：

函数图像：

函数的基本性质：

1、定义域：(−∞,+∞)(−∞,+∞)
2、值域：(−1,1)(−1,1)
3、函数在定义域内为连续和光滑函数
4、处处可导，导数为：f′(x)=f(x)(1−f(x))f′(x)=f(x)(1−f(x))
最早Logistic函数是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系时命名的。广义Logistic曲线可以模仿一些情况人口增长（P）的 S 形曲线。起初阶段大致是指数增长；然后随着开始变得饱和，增加变慢；最后，达到成熟时增加停止。1

二、 Sigmoid函数与逻辑回归
Sigmoid函数之所以叫Sigmoid，是因为函数的图像很想一个字母S。这个函数是一个很有意思的函数，从图像上我们可以观察到一些直观的特性：函数的取值在0-1之间，且在0.5处为中心对称，并且越靠近x=0的取值斜率越大。

机器学习中一个重要的预测模型逻辑回归（LR）就是基于Sigmoid函数实现的。LR模型的主要任务是给定一些历史的{X,Y}，其中X是样本n个特征值，Y的取值是{0,1}代表正例与负例，通过对这些历史样本的学习，从而得到一个数学模型，给定一个新的X，能够预测出Y。LR模型是一个二分类模型，即对于一个X，预测其发生或不发生。但事实上，对于一个事件发生的情况，往往不能得到100%的预测，因此LR可以得到一个事件发生的可能性，超过50%则认为事件发生，低于50%则认为事件不发生

从LR的目的上来看，在选择函数时，有两个条件是必须要满足的：
1. 取值范围在0~1之间。
2. 对于一个事件发生情况，50%是其结果的分水岭，选择函数应该在0.5中心对称。

从这两个条件来看，Sigmoid很好的符合了LR的需求。关于逻辑回归的具体实现与相关问题，可看这篇文章Logistic函数（sigmoid函数） – wenjun’s blog，在此不再赘述。

三、 为什么要选择Sigmoid函数？
很多文章讲到第二章就结束了，我们试着理解一下，第二章其实是在说LR模型可以选择Sigmoid函数实现，但是我们为什么选Sigmoid函数而不选择其他函数呢？这其实也是我一直困惑的点。例如仔细观察上述的两个条件，并不是只有Sigmoid能满足这两个条件，取值在0-1之间且以0.5值处中心对称的曲线函数有无数种。

我们可以从两个方面试着解释一下为什么选择Sigmoid函数。

LR的需求（选择Sigmoid是可以的）
上边我们从直观上说明了LR可以选择Sigmoid，下面从从数学上解释一下LR模型的原理。

对于一个分类模型，我们需要给定一个学习目标，对于LR模型来说，这个目标是最大化条件似然度，对于给定一个已知的样本向量x，我们可以表示其对应的类标记y发生的概率为P(y|x;w)P(y|x;w)，在此基础上定义一个最大似然函数学习w，就可以得到一个有效的LR分类模型。

仔细观察上述对LR的描述，LR模型的重点是如何定义这个条件概率P(y|x;w)P(y|x;w)。对于一个有效的分类器，通常上response value(响应值)即w⋅xw⋅x（w和x的内积）代表了数据x属于正类（y=1）的置信度。w⋅xw⋅x越大，这个数据属于正类的可能性越大；w⋅xw⋅x越小，属于反类的可能性越大。因此，如果我们有一个函数能够将w⋅xw⋅x映射到条件概率P(y=1|x;w)P(y=1|x;w)，而sigmoid函数恰好能实现这一功能（参见sigmoid的函数形状）：首先，它的值域是（0,1），满足概率的要求；其次，它是一个单调上升函数。最终，p(y=1|x，w)=sigmoid(w⋅x)p(y=1|x，w)=sigmoid(w⋅x)。sigmoid的这些良好性质恰好能满足LR的需求。2

Sigmoid特殊的性质（为什么选择Sigmoid）
这里给出两个解释：（个人感觉第二个更准确一点，不过真心看不懂）

正态分布解释
大多数情况下，并没有办法知道未知事件的概率分布形式，而在无法得知的情况下，正态分布是一个最好的选择，因为它是所有概率分布中最可能的表现形式。正态分布的函数如下：

在笛卡尔坐标系下，正态分布的函数呈现出“钟”形，如下图。图中四条曲线代表参数不同的四个正态分布。

在假定某个事件的概率分布符合正态分布的规律后，要分析其可能发生的概率，就要看它的积分形式，上图四个正态分布的曲线如图：

Sigmoid函数和正态分布函数的积分形式形状非常类似。但计算正态分布的积分函数，计算代价非常大，而Sigmoid的形式跟它相似，却由于其公式简单，计算量非常的小，因此被选为替代函数。3

最大熵解释
该解释是说，在我们给定了某些假设之后，我们希望在给定假设前提下，分布尽可能的均匀。对于Logistic Regression，我们假设了对于{X,Y}，我们预测的目标是Y|XY|X，并假设认为Y|XY|X服从bernoulli distribution，所以我们只需要知道P(Y|X)P(Y|X)；其次我们需要一个线性模型，所以P(Y|X)=f(wx)P(Y|X)=f(wx)。接下来我们就只需要知道f是什么就行了。而我们可以通过最大熵原则推出的这个f，就是sigmoid。4

这里给出推导过程，大神们可以看看，我是真没看懂：
LogisticRegressionMaxEnt.pdf

四、 总结
综上所述，Logistics Regression之所以选择Sigmoid或者说Logistics函数，因为它叫Logistics Regression。

没错，我是正经的，之所以这样说是因为问题在于，并不是只有Sigmoid函数能解决二分类问题。

为什么要选用sigmoid函数呢？为什么不选用其他函数，如probit函数？
其实，无论是sigmoid函数还是probit函数都是广义线性模型的连接函数（link function）中的一种。选用联接函数是因为，从统计学角度而言，普通线性回归模型是基于响应变量和误差项均服从正态分布的假设，且误差项具有零均值，同方差的特性。但是，例如分类任务（判断肿瘤是否为良性、判断邮件是否为垃圾邮件），其响应变量一般不服从于正态分布，其服从于二项分布，所以选用普通线性回归模型来拟合是不准确的，因为不符合假设，所以，我们需要选用广义线性模型来拟合数据，通过标准联接函数(canonical link or standard link function)来映射响应变量，如：正态分布对应于恒等式，泊松分布对应于自然对数函数，二项分布对应于logit函数（二项分布是特殊的泊松分布）。因此，说了这么多是想表达联接函数的选取除了必须适应于具体的研究案例，不用纠结于为什么现有的logistic回归会选用sigmoid函数，而不选用probit函数，虽然网上也有不少说法说明为什么选择sigmoid函数，例如“该函数有个漂亮的S型”，“在远离x＝0的地方函数的值会很快接近0/1”，“函数在定义域内可微可导”，这些说法未免有些“马后炮”的感觉，哪个说法仔细分析都不能站住脚，我觉得选用sigmoid函数也就是因为该函数满足分类任务，用的人多了也就成了默认说法，这跟给物体取名字有点类似的感觉，都有些主观因素在其中。5

逻辑函数 – 维基百科 ↩
知乎-为什么 LR 模型要使用 sigmoid 函数，背后的数学原理是什么？-谢澎涛的回答 ↩
Sigmoid什么鬼_ _ Shuping LIU ↩
知乎-为什么 LR 模型要使用 sigmoid 函数，背后的数学原理是什么？-匿名回答 ↩
机器学习－逻辑回归与最大似然估计 – Longfei Han ↩
———————
作者：狼血wolfblood
来源：CSDN
原文：https://blog.csdn.net/wolfblood_zzx/article/details/74453434
版权声明：本文为博主原创文章，转载请附上博文链接！