大家好,欢迎来到IT知识分享网。
最长回文子串
就是正着读与反着读都一样的字符串,在给定的字符串中寻找有这样性质而且长度最长的子串
例题
http://acm.hdu.edu.cn/status.php?user=jason6666&pid=3068
暴力法
#include<iostream> #include<cstdio> #include<string> #include<cstring> using namespace std; int findreversestring(string &s) { int len = s.length(); int maxlength = 0; int start; for (int i = 0; i < s.length(); i++)//遍历字符串 { for (int j = i + 1; j < s.length(); j++)//不停地截取字符串地子串 { int tmpi, tmpj; for (tmpi = i, tmpj = j; tmpi < tmpj; tmpi++, tmpj--) { if (s[tmpi] != s[tmpj])break; } if (tmpi >= tmpj&&j - i > maxlength)//如果满足tmpi >= tmpj表示这是一个回文串,而且满足j - i > maxlength表示这个子串地长度是目前最长的 { maxlength = j - i + 1;//更新长度 start = i;//更新起点 } } return maxlength;//返回长度(如果需要返回子串内容就return s,substr(i,maxlength);) } } int main() { std::ios::sync_with_stdio(false); std::cin.tie(0); std::cout.tie(0); string s; while (cin >> s) { cout << findreversestring(s) << endl; getchar(); } }
结果超时
动态规划法
#include<iostream> #include<cstdio> #include<string> #include<cstring> using namespace std; int findreversestring(string &s) { bool dp[110][110] = { false }; int len = s.length(); int maxlength = 0; int start; for (int i = 0; i < s.length(); i++)//初始化dp数组 { dp[i][i] = true; if (i < s.length() - 1 && s[i] == s[i + 1]) { dp[i][i + 1] = true;//先两个两个查看 start = i; maxlength = 2; } } for (int l = 3; l <= s.length(); l++)//不停的改变每次截取的字符串长度 { for (int i = 0; i <=s.length() - l; i++)//遍历整个字符串 { int j = i +l - 1;//子串的结尾地址 if (dp[i+1][j-1] && s[i] == s[j])//这里使用了动态规划的思想,也就是回文串的子串也是回文串,即如果满足dp[i+1][j-1]并且s[i] == s[j],则就是一个回文串 { dp[i][j] = true; start = i; maxlength = l;//改变串的长度 } } } return maxlength; } int main() { std::ios::sync_with_stdio(false); std::cin.tie(0); std::cout.tie(0); string s; while (cin >> s) { cout << findreversestring(s) << endl; getchar(); } }
Manacher(马拉车)算法
这个算法的总框架是,遍历所有的中心点,寻找每个中心点对应的最长回文子串,然后找到所有中心点对应的最长回文子串(即以各个字符为中心,改变半径寻找回文串的思想)
算法的使用前处理
由于算法使用的是回文串的特性,所以要求字符串的长度要是奇数,如果不是奇数的话就要对字符串进行填充,从而保证字符串为奇数。
代码
void init() { for (int i = 0; i <=len; i++)//len是初始字符串的长度 { str[2*i+1] = '#'; str[2*i+2] = s[i];//由于上面的界限是i<=len,所以str最后的字符是'\0' } str[0] = '*';//要保证字符串的第一个与最后一个是不同的 }
算法中参数的说明
1.len:初始字符串的长度
2.mx:当前回文串的最右边的边界
3.id:当前回文串的中心点
4.length数组,以每个字符为中心,能构成回文串的最大长度
算法的理解
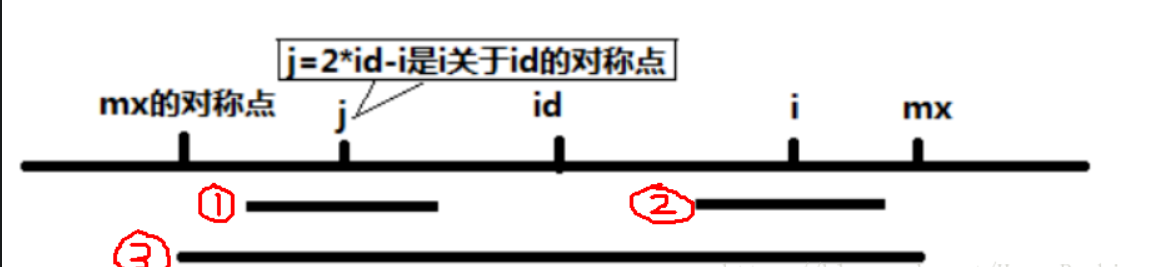
1.图的说明:id是回文串的中点,j是i关于id对称的点,其中j已经经过了遍历,所以length【j】是已知的
算法的总体思想我觉得就是使用已知的 length【j】来对length【i】进行判断 从而缩短算法的时间
2.首先判断i与mx的大小关系:
如果i大于mx,表示i现在所在的位置还没有经过判断,我们现在还不知道mx以外的字符是不是能够构成回文串,所以不能使用回文串的特点缩短判断,只能将length【i】置为1
如果i小于mx,就要讨论length【j】与mx-i之间的大小关系了(其实是两个半径的比较)
如果length【j】小于mx-i:表示图中的红1左边还没有超过mx的对称点,表示此时的length【j】是在整个大的回文串中的,我们可以使用回文串的性质得出length【i】=length【j】
如果length【j】大于mx-i:表示length【j】一部分已经在大的回文串外面,但是我们至少可以保证在length【j】中的mx-i这一段是ok的,所以length【i】=mx-i
算法代码
#include<iostream> #include<cstdio> #include<cstring> #include<string> #include<algorithm> using namespace std; int length[330000]; char str[330000], s[330000];//s中存放的是原始的字符串 int len,mx,id; void init() { for (int i = 0; i <=len; i++)//len是初始字符串的长度 { str[2*i+1] = '#'; str[2*i+2] = s[i];//由于上面的界限是i<=len,所以str最后的字符是'\0' } str[0] = '*';//要保证字符串的第一个与最后一个是不同的 } int Manachar() { int sum = 0, mx=0, id=0; length[0]=0; for (int i = 2; i < 2*len+1; i++)//遍历从2开始,因为0是*,1是# 都没有必要检测 添加后的str长度是2*len+1 { if (i < mx)length[i] = min(mx - i, length[2 * id - i]);//算法中最重要的一步 else length[i] = 1; while (str[i - length[i]] == str[i + length[i]])length[i]++;//这里在开始的时候在字符串的开始添加了*,保证数组不会越界 if (i + length[i]>mx)//一旦我们寻找的子串半径+i位置大于mx,就要更新mx的值 { mx = i + length[i]; id = i; sum = max(sum, length[i]); } } return sum - 1; } int main() { while (scanf("%s",s)!=EOF) { len = strlen(s); init(); cout << Manachar() << endl; getchar(); } }
参考:https://blog.csdn.net/HappyRocking/article/details/82622881?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/30682.html