三角函数的定义

大家好，欢迎来到IT知识分享网。

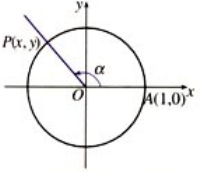
利用单位圆来定义任意角的三角函数，如下图所示，$\alpha$ 是一个任意角，它的终边与单位圆交于点 $P(x,y)$。

那么角 $\alpha$ 的正弦定义为

$$\sin \alpha = y$$

角 $\alpha$ 的余弦定义为

$$\cos \alpha = x$$

角 $\alpha$ 的正切定义为

$$\tan \alpha = \frac{y}{x}$$

周期性在图像上可以直观看出，点 $P$ 从 $A$ 点出发绕 $360$ 度后又回到起始点。

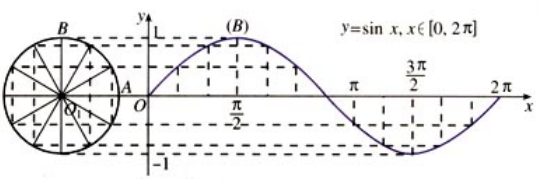
角 $\alpha$ 的正弦图像如下：

可以看出，正弦函数的定义就是：单位圆上点的纵坐标与角度(弧度表示)的关系，这个角度是该点与原点的连线和 $x$ 轴正半轴的夹角。

角频率：表示单位时间内变化的角度弧度值，单位为 $rad/s$。

现在我们将正弦函数中角度的变化表示为角频率和时间的乘积，即 $\alpha = \omega t$，所以

$$f = \sin\alpha = \sin \omega t$$

可以发现，当 $\omega = 1 \; rad/s$ 时，$t$ 在数值上就等于 $\alpha$。

接下来研究下面这个函数

$$f(t) = A\sin(\omega t + \varphi)$$

函数 $f = \sin \alpha$ 的周期就是圆周的角度，即 $2\pi$，转化为角速度乘上时间之后，函数 $f(t)$ 的周期就是角度变化一个圆周的时间，所以

$$T = \frac{2\pi}{\omega}$$

频率：函数每秒钟完成周期性变化的次数，所以有

$$f = \frac{1}{T}$$

所以

$$\omega = 2\pi f$$