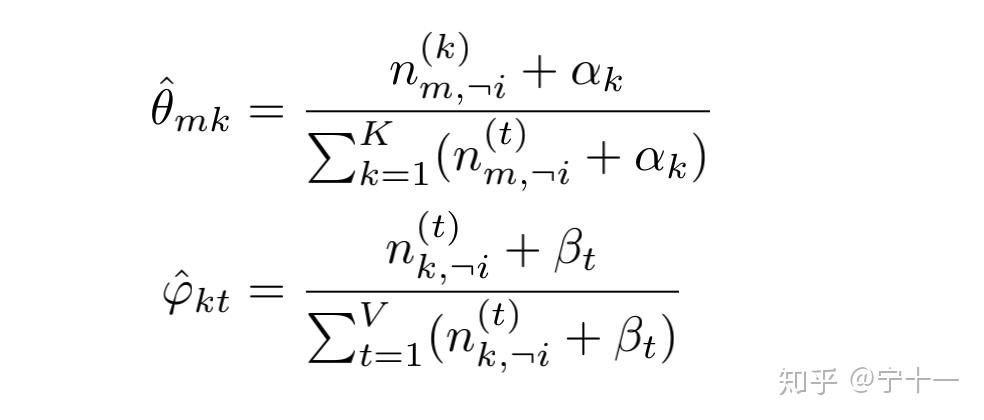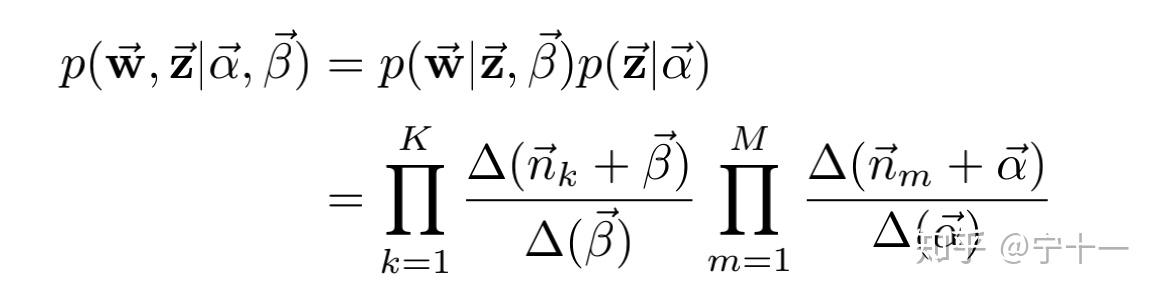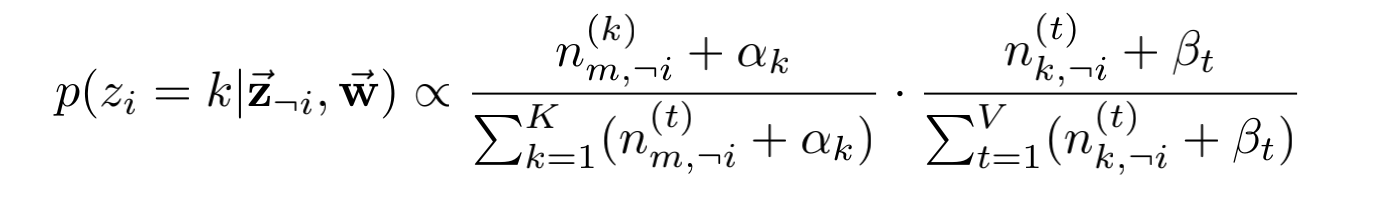什么是BTM?

大家好，欢迎来到IT知识分享网。

　记录学习BTM 来源知乎等https://zhuanlan.zhihu.com/p/111545954

什么是BTM

BTM和LDA一样都是主题模型，就是给你一篇文档，你指定一个主题的个数，这两个模型都会生成每个主题中的关键词，以及一篇新的文档中各个主题的概率有多大。根据论文作者的表述。传统的主题模型（LDA）在处理短文本（比如直播间弹幕，微博文本等等），会因为文本中的词过于稀疏，得到模型的效果不够好。为了解决这个问题。大佬们提出一种新的主题模型，就是BTM，而且BTM论文的作者说，在短文本上BTM的表现要比LDA好，即使是长文本，BTM的效果也不比LDA弱。

BTM的英文全名叫(Biterm Topic Model），这里一共三个单词，我觉的大家肯定认识后面两个，那我给大家解释下第一个吧，Biterm翻译成什么我也不知道，但是这不并不影响我们理解论文，我给大家举个例子大家就明白了。我们这里有一句话 “清风明月，草长莺飞，杨柳依依“，这里假设我们断句分词后得到三个词.

['清风明月','草长莺飞','杨柳依依']

那么，这句话就包括三个biterm，分别是

['清风明月','草长莺飞'] ['杨柳依依','草长莺飞']['清风明月','杨柳依依']

这里假设大家都了解LDA的建模过程，如果不了解的话，墙裂建议大家去看《数学八卦》,有哪里不懂，可以私信我，反正我不一定会。我们知道LDA是根据单个单词去建模。而BTM的不同之处就在于，BTM是根据上面的biterm来建模的。这里再举个例子。在上面的句子中，假如是用LDA建模，那么我们在建模的时候，会假设清风明月 属于主题一，杨柳依依属于主题二，草长莺飞属于主题三这种，但是在BTM中，我们假设biterm1 属于主题1 ，biterm2属于主题2这种。基本这就是这两个模型的区别了，其他的几乎都一样，一样使用Dir-Multi共轭建模，一样使用Gibbs求解（只是我个人的理解，可能略显肤浅，各位老板轻喷）。

为什么LDA不适合做短文本分析

这个是在知乎的另一位大佬那里看来的。担心大家懒，不想去点，我在这里复述一遍。

https://www.zhihu.com/question/313275693/answer/605783460

假设大家都读了LDA数学八卦，在数学八卦的第54页，有两个更新多项分布参数的 公式。我这里贴一下。

  表示的是第m篇文档中，各个单词的主题。 这里的i是一个二维变量（m,n)表示第m篇文档中的第n个词，m表示第m篇文档，k表示第k个主题， 所以这个的含义就是在第m篇文档中除去第i(m,n)个词的第k个主题产生的单词个数。而根据经验，这个词汇的个数是根据MCMC仿真出来的，随机性较大，由于文本特征很少，那么大多数主题的词频计数可能都是0，同时，其他极少数主题对应的词频计数为1（一个句子的词汇个数很有可能没有主题多），此外，由于我们对Dirichlet的参数一无所知，因此一般的设置  为相等的。结合以上两点，参数估计的严重问题就产生了。当给予先验参数较大权重的时候，文本较短导致文本内容对参数估计提供的有价值信息局限了。可想而知，  基本上都依赖与Dirichlet的先验参数  ，等概率的参数导致结果基本上都是均匀的向量，没有分类的意义;当给与的先验参数较小权重时，由于取值为1的主题很少，随机性又很大，导致主题很难广泛低分布在多个主题上，倾向于聚集在1到2个主题上，当我们一个主题模型只有一个主题的时候，那这个主题模型存在的意义可能是不大了。。。

为什么BTM更适合做短文本分析

综合上面说的，我们知道，BTM和LDA除了使用biterm建模外，其余的几乎和LDA相同，而问题就在这个Biterm上了。LDA存在的问题是当文本过短的时候，比如一个文本只有10个单词，那么模型可能会很差，但是，在BTM中，即使一个文本中只有10条单词，那么也会有45个biterm（高中的排列组合）很好的解决了LDA对短文本存在的问题。而且论文中说，显而易见，使用biterm（两个词）对文本建模要比一个词建模要能更好的显示文章的隐藏主题（它这个显而易见，就和高中做数学题。答案给的是 易得 一样。。。）

参数的更新（数学公式预警）

上面说过，除了建模的方式，LDA和BTM几乎都是一样的（这句话说过好多遍了），论文中使用的Gibbs更新的参数，所以这里我们先草草的过一遍LDA求解参数的方法 ，首先我们假设大家都知道在传统的LDA中有M+K的Dir-Multi共轭分布，Gibbs采样，我们这里先简单回顾下LDA主题模型中求  和  的方法，为了能够完成Gibbs采样，我们需要一个条件概率，而为了求这个条件概率， 我们又需要联合概率。这个联合概率就是通过Dir-Multi求得的。

LDA中联合概率的计算公式，数学八卦第49页

上面的公式中，  和  是我们给定的伪计数， 表示的是第k个topic产生的每个单词的个数，比如  表示的是1号主题产生的2号单词的个数。 表示的第m篇文档中第k个topic产生的词的个数。有了上面的联合分布，我们就可以求条件分布，进而进行Gibbs采样了。我们经过推导（此处略去3亿个脑细胞）。得到了下面的条件概率公式

LDA中的条件概率公式，数学八卦第51页

我们对按照上面的公式进行Gibbs采样，更新每个词对应的topic，重复操作，知道Gibbs sampling收敛，得到完整的模型。

上面复习了在LDA中更细参数的方法后我们回到主题看一下BTM是如何更新参数的。贴上伪代码和公式更新的结果，图片来自论文（A Biterm Topic Model for Short Text)

算法的伪代码Gibbs采样中用到的条件概率根据采样结果，求出概率的公式

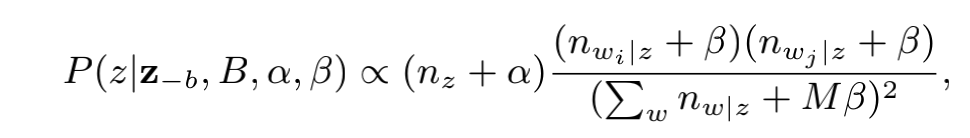
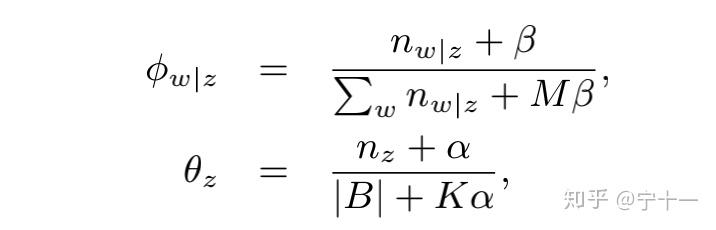
我们可以看到BTM的参数更新方式和LDA几乎相同除了在Gibbs采样的时候是求的biterm的条件概率，然后更新参数，哦，对，这里说一下，如果一个biterm属于主题1，那么biterm中的每个词都属于主题1 。 剩下的几乎和LDA没有区别，公式中的变量也和之前LDA中的差不多。大家想深入了解的。可以自己去读读BTM的论文。还是那句话，如果有问题，可以私信我。

后记

在之前的LDA文章中，有小伙伴问我，要怎么计算  和  ，这个其实挺不好算的。因为需要太多的前置数学知识。我会抽空整理下，尽量用通俗的语言把这个写一篇笔记出来吧。这篇文章讲的并不深入，如果大家想深入了解BTM，还是需要自己静下心来来认真读读教材和论文。当然，我也有一些地方不是特别理解，这篇文章更像是自己的读书笔记，如果能帮到你，万分荣欣，如果不幸让你更迷茫了或者写错了，那深感抱歉，如果大家遇到了问题，欢迎大家私信我，我们可以一起研究。