大家好,欢迎来到IT知识分享网。
一.线性方程组求解定理
1.线性方程组有解判别定理 线性方程组
a11 x1 + a12 x2 + … + a1n x n = b1 ,
a21 x1 + a22 x2 + … + a2n x n = b2 ,
………………………………………………
as1 x1 + as2 x2 + … + asn x n = bs
有解的充分必要条件是 : 它的系数矩阵与增广矩阵有相同的秩 .
2. 齐次线性方程组
a11 x1 + a12 x2 + … + a1n x n = 0 ,
a21 x1 + a22 x2 + … + a2n x n = 0 ,
………………………………………………
as1 x1 + as2 x2 + … + asn x n = 0
有非零解的充分必要条件是: 它的系数矩阵的秩 r 小于未知量个数 n .
齐次线性方程组求解一般步骤:
1.把系数矩阵通过初等变换,变换成阶梯形矩阵.
2.判断阶梯形矩阵中非零行的个数秩(r),以及计算自由元个数m=n-r.
3.确定自由元位置,然后以次为它们赋值1,0…
4.求解出方程组的基础解系.
5.用基础解系表示出方程全解.
非齐次线性方程组求解,与齐次线性方程组求解过程基本一致,只需要再求出一个特解。
二.如何用C语言计算线性方程组的解
那么如何用算法求出线性方程组的解呢?
就是根据上面方程组求解一般步骤来的,
1.矩阵的初等变换(在上次行列式计算的基础上,这个很好实现).
2.求出矩阵的秩/自由元个数,然后确定自由元的位置(我认为这是一个难点)
3.初始化自由元(1,0,..),计算变量,最终求出基础解系
4.非齐次线性方程
4.1.先求出齐次线性方程组的基础解系
4.2.再利用上面步骤求一个特解即可
1.矩阵的初等变换
//初等行变换 void primaryRowChange(int s, int n, double **array) { int i,j,k,ii,kk,flag; double temp; for(i=0,j=0;i<s-1;i++,j++)//s行,最外围只需要变换s-1 { ii=i; //如果行的首元为0,向下查找一个不为0的,然后换行 if(*(*(array+i)+j) == 0) { flag=0; for(k=i+1;k<s;k++) { if(*(*(array+k)+j)!=0)//第k行与第i行交换 { for(kk=j;kk<n;kk++) { temp=*(*(array+k)+kk); *(*(array+k)+kk) = *(*(array+i)+kk); *(*(array+i)+kk) = temp; } flag =1; break; } } //判断是交换成功,如果没有成功,则i-- if(!flag) { i--; continue; } i--; j--; continue; } for(;ii<s-1;ii++) { if(*(*(array+ii+1)+j)==0) continue; temp =-*(*(array+ii+1)+j) / *(*(array+i)+j); for(k=j;k<n;k++) *(*(array+ii+1)+k) += *(*(array+i)+k) * temp; } } }
2.计算矩阵的秩
//计算矩阵的秩 int getRank(int s, int n, double **array) { int flag; int i,j,r=s; //判断非零行个数 for(i=0;i<s;i++) { flag=0; for(j=0;j<n;j++) { if(*(*(array+i)+j)!=0 && (*(*(array+i)+j)>0.01 || *(*(array+i)+j) <-0.01))//排除很小数, { flag=1; break; } } if(!flag)//当前行全为零,则r为i; { r=i; break; } } return r; }
3.确定自由元位置
自由元确定需要考虑两种情况:
1).系数梯形矩阵最后一行只有一个非零元素.
2) 系数梯形矩阵中某行的个数等于自由元的个数.
//获取自由元信息 int* getFreeElement(int r, int n, double **array, int **matrixPrimary, double **matrixCalc) { int i,j,k,o,p,q; int m=n-1-r;//n-1: int *freeElement =(int*)malloc(m*sizeof(int)); j=-1;//判断是否有为0的变量 q=0;//如果当前行非零个数与自由元个数相等,则标记为1,自由元选择起始位置左移一位 for(i=r-1;i>=0;i--)//查找自由元,及位置为0的 { if(*(*(matrixPrimary+i)+1)==1)//说明第i行只有一个变量,如果是齐次方程它的解一定为0 { j=*(*(matrixPrimary+i)+0); for(k=0;k<r;k++) *(*(matrixCalc+k)+j)=*(*(array+k)+n-1) / *(*(array+k)+j); } else if(n-1-matrixPrimary[i][0]==m) { q=1; } else if(n-1-matrixPrimary[i][0]>m) { o=matrixPrimary[i][0];//当前行的首元位置 p=0;//次数 for(k=n-2-q;k>=o;k--)//从后向前查找自由元位置 { if(k==j) continue; freeElement[p++]=k; if(p==m)//说明已经找到 m个自由元 return freeElement; } } } return freeElement; }
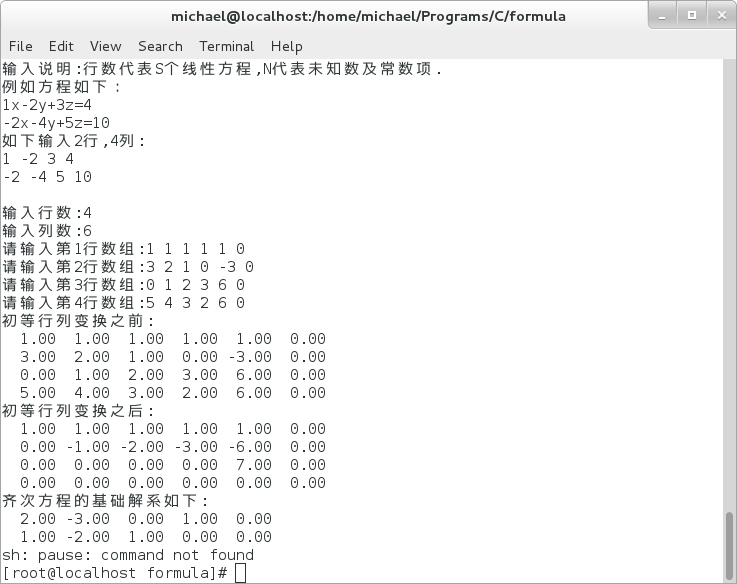
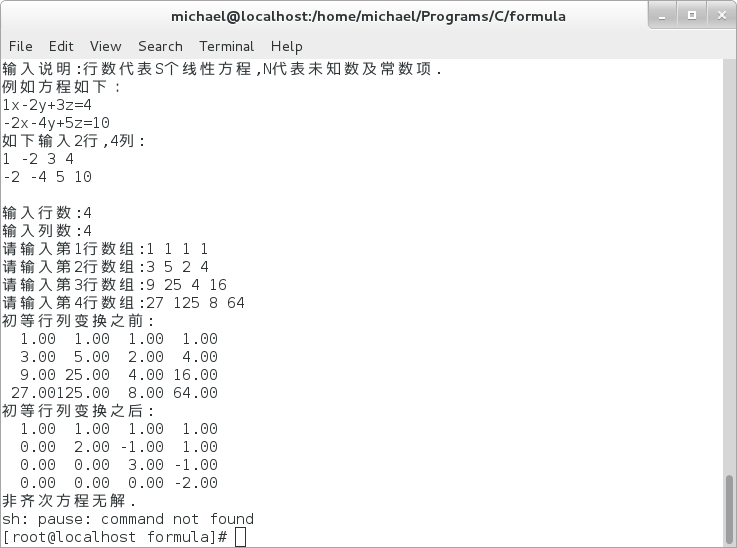
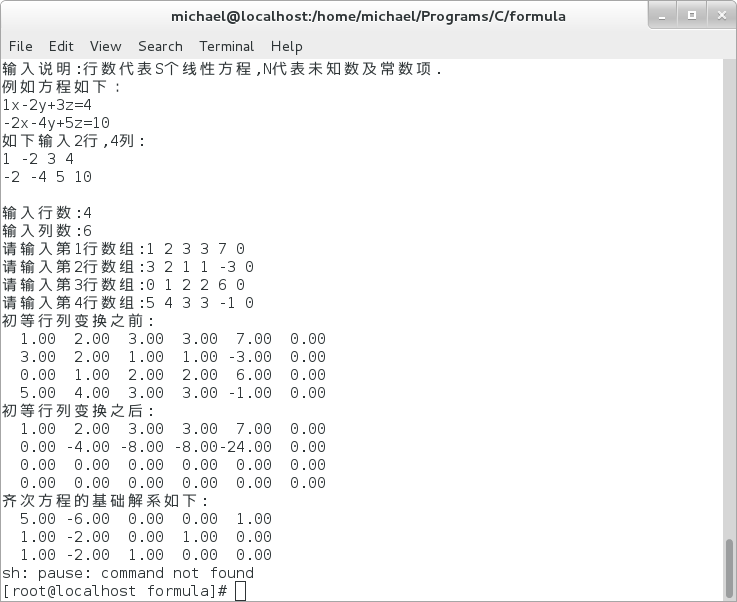
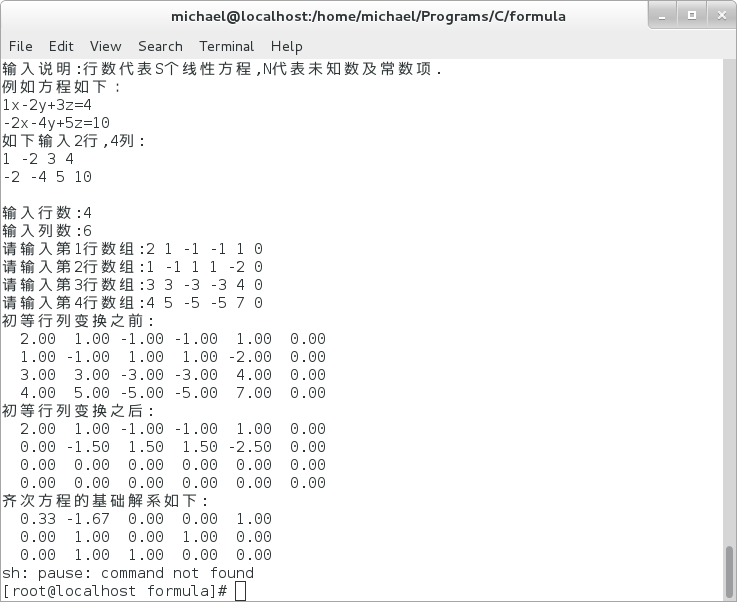
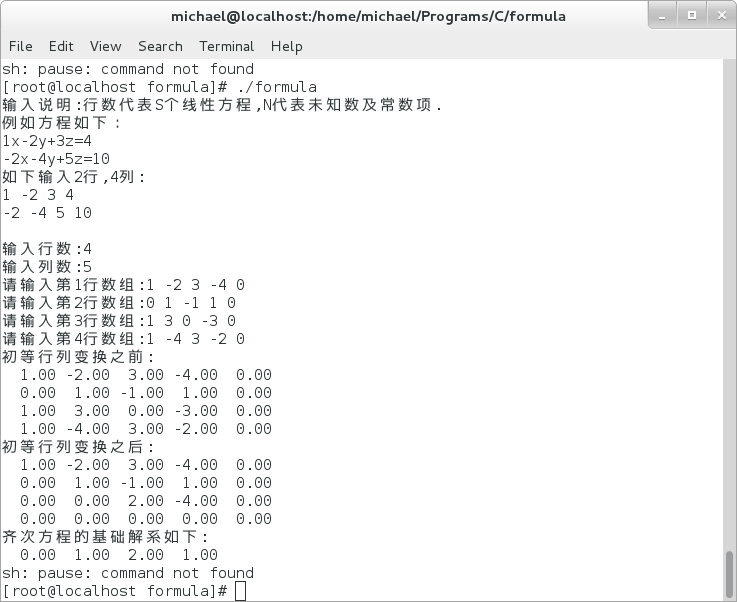
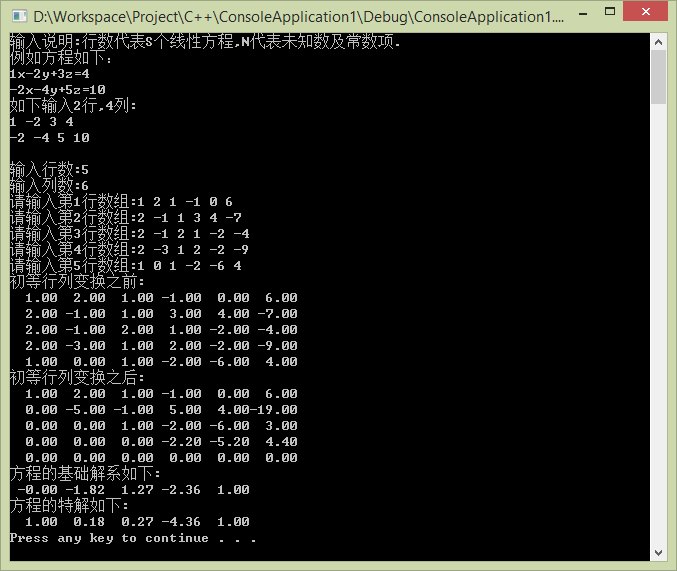
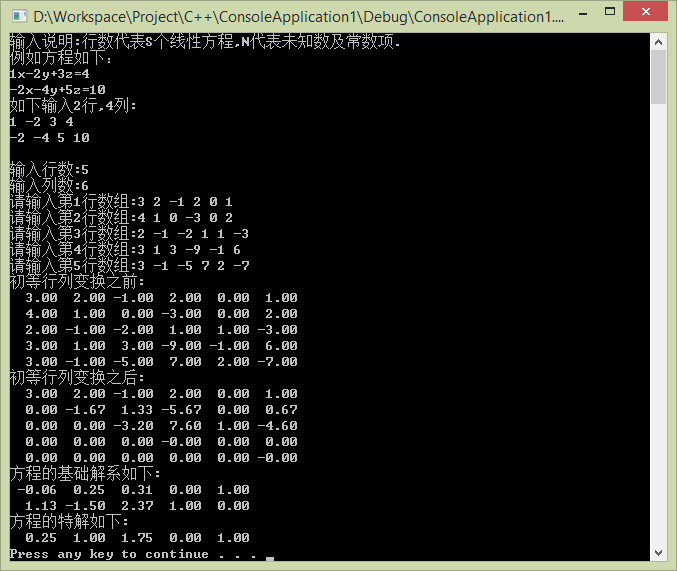
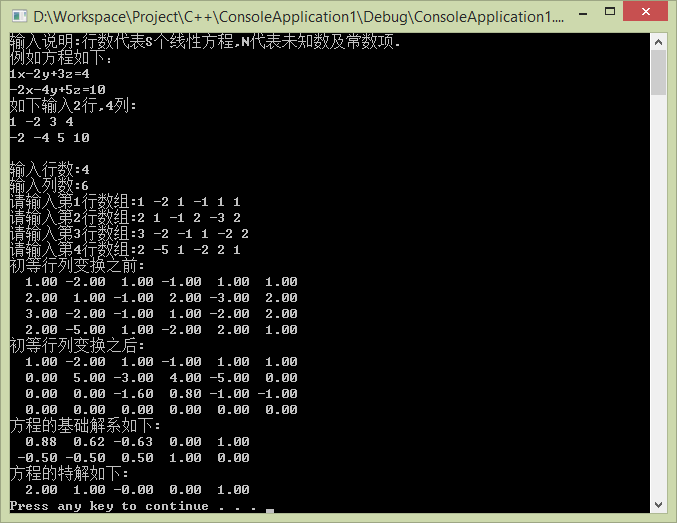
求解示例图:
1> p148-例4
2> 2.7(1)-1
3> 2.7(2)-1.1
4> 2.7(2)-1.2
5> 2.7(2)-1.3
6> 2.7(3)-1.1
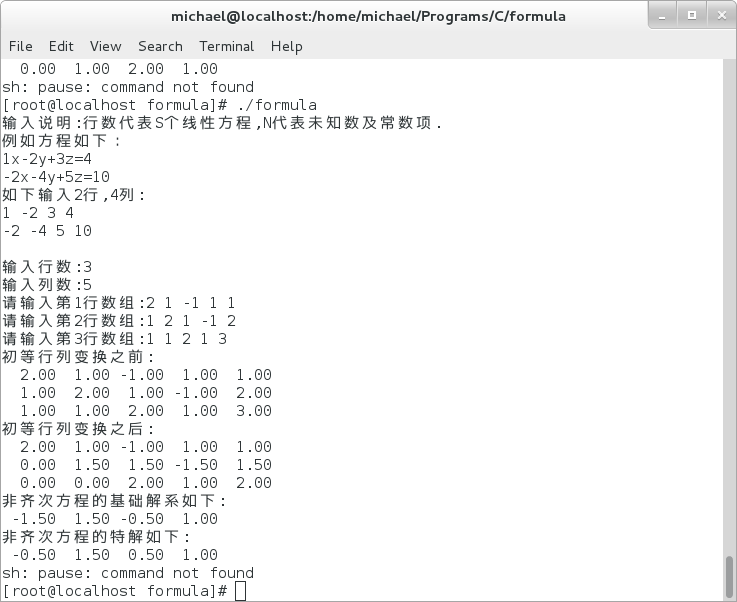
7> 2.7(3)-1.2
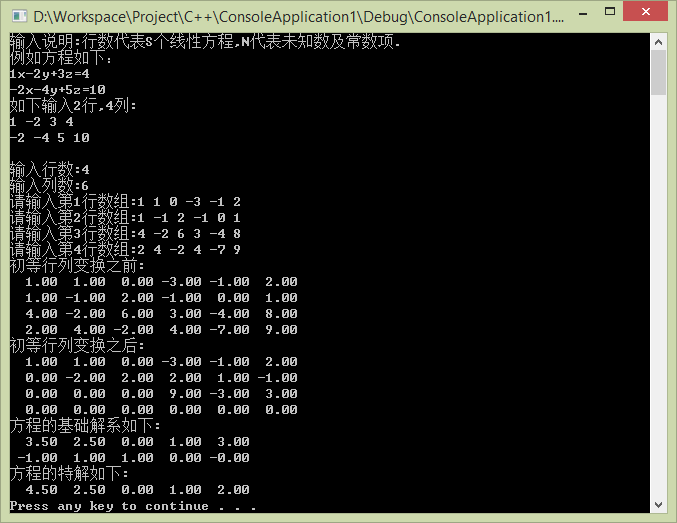
8> 2.7(3)-1.3
9> 2.7(3)-1.4
10> p155-例6
以下是C语言求解的全部源代码


#include <stdio.h> #include <stdlib.h> double undefined=-999;//标志位 void main() { int i,j,s,n; int res; double **array,*temp,**result; double *special;//特解 //temp double t1[6]={1,1,1,1,1,0}; double t2[6]={3,2,1,0,-3,0}; double t3[6]={0,1,2,3,6,0}; double t4[6]={5,4,3,2,6,0}; int homogeneous=1;//标识方程是否是齐次方程 void primaryRowChange(int s, int n, double **array); void printfDouble1Dimension(int n, double *array); void printfDouble2Dimension(int s, int n, double **array); int homogeneousResolve(int s, int n, int homogeneous, double **array, double **result); int nonHomegeneousResolve(int s, int n, double **array, double **result,double *special); //void printfInt2Dimension(int s, int n, int ** array); //int* getPrimary(int n,double *temp); //输入说明 printf("输入说明:行数代表S个线性方程,N代表未知数及常数项.\n"); printf("例如方程如下:\n"); printf("1x-2y+3z=4\n"); printf("-2x-4y+5z=10\n"); printf("如下输入2行,4列:\n"); printf("1 -2 3 4\n"); printf("-2 -4 5 10\n\n"); //开始 printf("输入行数:"); scanf("%d",&s); printf("输入列数:"); scanf("%d",&n); //s=4; //n=6; //动态分配内存空间 array =(double**)malloc(s*sizeof(double*)); result =(double**)malloc(s*sizeof(double*)); special =(double*)malloc(n*sizeof(double)); for(i=0;i<s;i++) { temp=(double*)malloc(n*sizeof(double)); printf("请输入第%d行数组:",i+1); for(j=0;j<n;j++) scanf("%lf",temp+j); /* switch(i) { case 0: temp=t1;//{1,1,1,1,1,0}; break; case 1: temp=t2;//{3,2,1,0,-3,0}; break; case 2: temp=t3;//{0,1,2,3,6,0}; break; case 3: temp=t4;//{5,4,3,2,6,0}; break; }*/ array[i]=temp; } //打印数组 printf("初等行列变换之前:\n"); printfDouble2Dimension(s,n,array); //判断方程是否是齐次方程 for(i=0;i<s;i++) { if(*(*(array+i)+n-1)!=0)//如果最后一列,有不为0的 说明方程为非齐次方程 { homogeneous=0; break; } } primaryRowChange(s,n,array); printf("初等行列变换之后:\n"); printfDouble2Dimension(s,n,array); if(homogeneous)//齐次 { res = homogeneousResolve(s, n, homogeneous, array, result); switch (res) { case -1: printf("方程无解.\n"); break; case 0: printf("方程只有零解.\n"); break; default: printf("方程的基础解系如下:\n"); printfDouble2Dimension(res,n-1,result); break; } } else//非齐次 { res=nonHomegeneousResolve(s,n,array,result,special); if(res==-1) printf("方程无解.\n"); else { printf("方程的基础解系如下:\n"); printfDouble2Dimension(res,n-1,result); printf("方程的特解如下:\n"); printfDouble1Dimension(n-1,special); } } system("pause"); } //初等行变换 void primaryRowChange(int s, int n, double **array) { int i,j,k,ii,kk,flag; double temp; for(i=0,j=0;i<s-1;i++,j++)//s行,最外围只需要变换s-1 { ii=i; //如果行的首元为0,向下查找一个不为0的,然后换行 if(*(*(array+i)+j) == 0) { flag=0; for(k=i+1;k<s;k++) { if(*(*(array+k)+j)!=0)//第k行与第i行交换 { for(kk=j;kk<n;kk++) { temp=*(*(array+k)+kk); *(*(array+k)+kk) = *(*(array+i)+kk); *(*(array+i)+kk) = temp; } flag =1; break; } } //判断是交换成功,如果没有成功,则i-- if(!flag) { i--; continue; } i--; j--; continue; } for(;ii<s-1;ii++) { if(*(*(array+ii+1)+j)==0) continue; temp =-*(*(array+ii+1)+j) / *(*(array+i)+j); for(k=j;k<n;k++) *(*(array+ii+1)+k) += *(*(array+i)+k) * temp; } } } //非齐次方程解的情况 int nonHomegeneousResolve(int s, int n, double **array, double **result, double *special) { int i,j,k,l; int r1,r2;//系数矩阵/增广矩阵的秩 double **temp ;//用来存储特解 int getRank(int s, int n, double **array); int homogeneousResolve(int s, int n, int homogeneous, double **array, double **result); r1=getRank(s,n-1,array); r2=getRank(s,n,array); if(r1!=r2) return -1;//无解 //特解 temp =(double**)malloc(r1*sizeof(double*)); homogeneousResolve(r1,n,0,array,temp); for(i=0;i<n;i++) *(special+i)=*(*(temp)+i); return homogeneousResolve(r1,n,1,array,result); } //齐次方程解的情况 int homogeneousResolve(int s, int n, int homogeneous, double **array, double **result) { int i,j,k,l,o,p,flag; int r;//秩rank int m;//自由元个数 int f;//最后一个非零行首元的位置 double sum1=0,sum2=0; double *temp = (double*)malloc(n*sizeof(double));//临时行指针 int **matrixPrimary;//存储矩阵首元位置及非零元个数 double **matrixCalc;//计算基础解系 int *freeElement;//自由元位置 double **matrixTemp; //声明函数 void printfDouble2Dimension(int s, int n, double **array); void printfInt2Dimension(int s, int n, int **array); int** getPrimary(int s, int n, double **array); int getRank(int s, int n, double **array); double** initMatrixCalc(int s, int n); int* getFreeElement(int r, int n,double **array, int **matrixPrimary, double **matrixCalc); void printfInt1Dimension(int n, int *array); void getPrimarySolution(int r, int n, int homogeneous, double **array, int **matrixPrimary, double **matrixCalc ,int *freeElement, double **result); //秩rank r = getRank(s,n,array); //判断解的情况 m=n-1-r; if(m<0) return -1;//无解 else if(m==0) return 0;//只有零解 else { //初始化计算矩阵 matrixCalc = initMatrixCalc(r,n); //获取矩阵首元信息 matrixPrimary = getPrimary(r,n,array); /*printf("打印计算矩阵:\n"); printfDouble2Dimension(r,n,matrixCalc); printf("打印矩阵首元信息:\n"); printfInt2Dimension(r,2,matrixPrimary); */ freeElement = getFreeElement(r, n, array, matrixPrimary,matrixCalc); //打印自由元位置 //printf("打印自由元位置:\n"); //printfInt1Dimension(m, freeElement); //计算基础解系 getPrimarySolution(r, n, homogeneous, array, matrixPrimary, matrixCalc, freeElement ,result); //printfDouble2Dimension(m,n,result); return m; } } //init Matrix calc double** initMatrixCalc(int s, int n) { int i,j; double **array=(double**)malloc(s*sizeof(double*)); for(i=0;i<s;i++) { array[i] =(double*)malloc(n*sizeof(double)); *(*(array+i)+n-1)=1; for(j=0;j<n-1;j++) { *(*(array+i)+j)=undefined; } } return array; } //计算矩阵的秩 int getRank(int s, int n, double **array) { int flag; int i,j,r=s; //判断非零行个数 for(i=0;i<s;i++) { flag=0; for(j=0;j<n;j++) { if(*(*(array+i)+j)!=0 && (*(*(array+i)+j)>0.01 || *(*(array+i)+j) <-0.01))//排除很小数, { flag=1; break; } } if(!flag)//当前行全为零,则r为i; { r=i; break; } } return r; } //查找某行非零个数及首元位置 int** getPrimary(int s, int n, double **array) { int i,j; int num=0,index=0; int **result=(int**)malloc(s*sizeof(int*)); int *temp; for(i=0;i<s;i++) { temp =(int*)malloc(2*sizeof(int)); num=0; index=0; for(j=0;j<n;j++) { if(*(*(array+i)+j)!=0) { if(num==0) index=j; num+=1; } } temp[0]=index; temp[1]=num; result[i]=temp; } return result; } //获取自由元信息 int* getFreeElement(int r, int n, double **array, int **matrixPrimary, double **matrixCalc) { int i,j,k,o,p,q; int m=n-1-r;//n-1: int *freeElement =(int*)malloc(m*sizeof(int)); j=-1;//判断是否有为0的变量 q=0;//如果当前行非零个数与自由元个数相等,则标记为1,自由元选择起始位置左移一位 for(i=r-1;i>=0;i--)//查找自由元,及位置为0的 { if(*(*(matrixPrimary+i)+1)==1)//说明第i行只有一个变量,如果是齐次方程它的解一定为0 { j=*(*(matrixPrimary+i)+0); for(k=0;k<r;k++) *(*(matrixCalc+k)+j)=*(*(array+k)+n-1) / *(*(array+k)+j); } else if(n-1-matrixPrimary[i][0]==m) { q=1; } else if(n-1-matrixPrimary[i][0]>m) { o=matrixPrimary[i][0];//当前行的首元位置 p=0;//次数 for(k=n-2-q;k>=o;k--)//从后向前查找自由元位置 { if(k==j) continue; freeElement[p++]=k; if(p==m)//说明已经找到 m个自由元 return freeElement; } } } return freeElement; } //计算基础解系 void getPrimarySolution(int r, int n, int homogeneous, double **array, int **matrixPrimary, double **matrixCalc ,int *freeElement, double **result) { int i,j,k,l,p; int m=n-1-r;//自由元 double sum1,sum2; double *temp,**matrixTemp; //计算基础解系 for(i=0;i<m;i++) { matrixTemp=(double**)malloc(r*sizeof(double*)); //复制数组 for(j=0;j<r;j++) { temp =(double*)malloc(n*sizeof(double)); for(k=0;k<n;k++) *(temp+k)=*(*(matrixCalc+j)+k); matrixTemp[j]=temp; } //设置自由元为0或1 for(j=0;j<r;j++) { *(*(matrixTemp+j)+freeElement[i])=1;//自由元为1 for(k=0;k<m;k++) { if(k!=i) *(*(matrixTemp+j)+freeElement[k])=0;//自由元为0 } } //printfDouble2Dimension(r,n,matrixTemp); //计算 for(j=r-1;j>=0;j--) { p=*(*(matrixPrimary+j));//当前行起始位置 for(k=p;k<n;k++) { if(*(*(matrixTemp+j)+k)==undefined)//如果等于标志位,它可能是未知变量 { sum1=sum2=0; for(l=p;l<n;l++) { if(l==n-1) { sum1=*(*(array+j)+l) * *(*(matrixTemp+j)+l); } else if(l!=k) { sum2+=*(*(array+j)+l) * *(*(matrixTemp+j)+l); } } for(l=0;l<r;l++) *(*(matrixTemp+l)+k)=((homogeneous?0:sum1)-sum2)/ *(*(array+j)+k);//如果齐次sum1=0; //break; } } } result[i]=matrixTemp[0]; //printfDouble2Dimension(r,n,matrixTemp); } } //打印数组 void printfDouble2Dimension(int s, int n, double **array) { //printf("%d,%d",s,n); int i,j; for(i=0;i<s;i++) { for(j=0;j<n;j++) { printf("%6.2lf",*(*(array+i)+j)); } printf("\n"); } } void printfDouble1Dimension(int n, double *array) { int i; for(i=0;i<n;i++) { printf("%6.2lf",*(array+i)); } printf("\n"); } //打印二维数组 void printfInt2Dimension(int s, int n, int **array) { int i,j; for(i=0;i<s;i++) { for(j=0;j<n;j++) { printf("%4d",*(*(array+i)+j)); } printf("\n"); } } //打印一维数组 void printfInt1Dimension(int n, int *array) { int i; for(i=0;i<n;i++) { printf("%4d",*(array+i)); } printf("\n"); }
View Code
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/32845.html