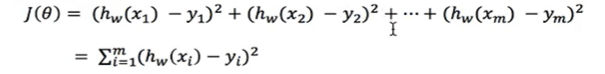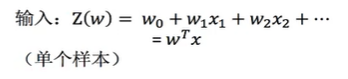大家好，欢迎来到IT知识分享网。

线性回归和逻辑回归

一 线性回归：

1.线性回归就是寻找一种能预测的趋势

2.线性关系：二维-直线关系

​ 三维-特征，目标值

3.线性关系的定义：y = kx + b b-偏置值，为了是对于单个特征的情况更加通用

多个特征：k1*房子面积+k2房子位置+b

通过属性的线性组合来预测的函数：f(x) = w1x1+w2x2+…+wdxd+b

w为权重，b为偏置项

4.数组和矩阵的特点 :

(1) 数组

0维 5

1维 [1,2,3,4,5]

2维 [[1,2,3,4,5],[7,8,9,4,5]]

3维 [[[1,2,3],[1,2,3]],[[1,2,3],[1,2,3]]]

数组：numpy:ndarray

(2) 矩阵：

必须是二维，矩阵乘法：(m行,l列)*(l行,n列)=(m行,n列)

特征值 权重 目标值

[[1,2,3,4]] [[2],[2],[2],[2]] 一个样本应该是一个值

(100,4) (4,1) (100,1)

矩阵乘法：满足特定运算的需求

属性和权重的一种组合来预测结果

5.线性回归策略

(1) 统计学习方法：算法，策略（损失函数），优化

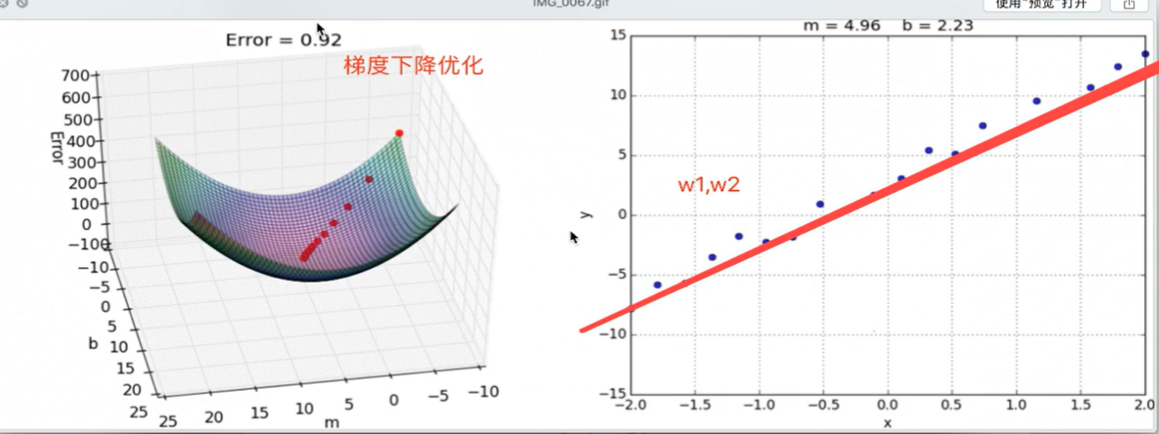
(2) 梯度下降：

w和b

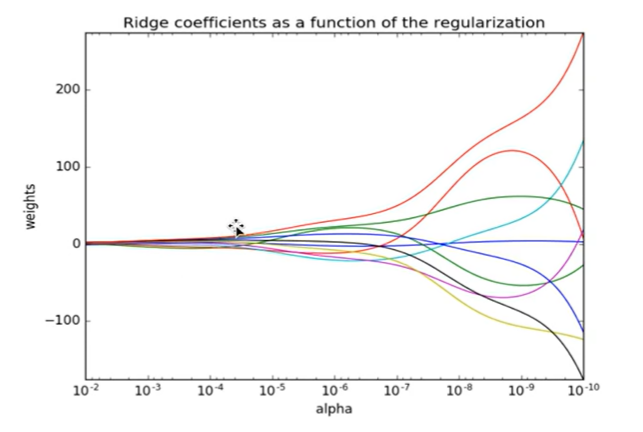
(3) 岭回归：

回归得到的回归系数更符合实际，更可靠。

能让估计的参数波动范围变小，变稳定，在存在病态数据偏多的研究中有较大的实用价值。

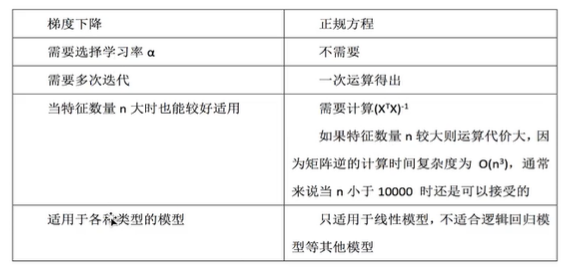
6.线性回归API：

正规方程：sklearn.linear_model.LinearRegression

梯度下降：sklearn.linear_model.SGDRegressor

coef_:回归系数

就是寻找最优化的w值

7.线性回归的一些问题:

(1) 对数据进行标准化处理 x y都需要

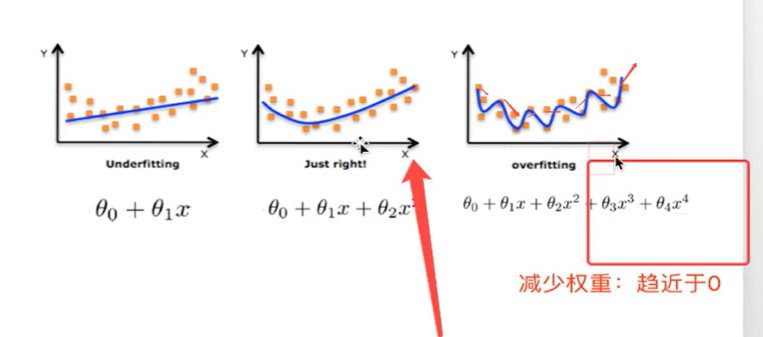
(2) 过拟合和欠拟合

小规模数据 LinerRegression(不能解决拟合问题)

大规模数据 SGDRegression

​ -欠拟合是测试误差和训练误差都大【模型过于简单】

​ -过拟合是训练误差小，测试误差大 【模型过于复杂】

​ 通过交叉验证训练集结果，看训练集和测试集的表现

(3) 特征选择：

过滤式：低方差特征

嵌入式：正则化，决策树，神经网络

自动调整参参数，尽量减少高次项的特征影响。

解决过拟合的方法：

L2正则化：使得w的元素都很小，接近于0

Ridge：岭回归，带有正则化的线性回归，解决过拟合

岭回归api:

 sklearn.linear_model.Ridge(alpha=1.0)：具有l2正则化的线性最小二乘法

alpha：正则化力度 coef_：回归系数

8.房价预测的例子

def mylinear():
    # 线性回归预测房子的价格

    # 获取数据
    lb = load_boston()
    # 划分训练集
    x_train,x_test,y_train,y_test = train_test_split(lb.data,lb.target,test_size=0.25)

    print(y_train)
    # 进行标准化 目标值是否要进行标准化处理？
    # 特征值缩小，目标值也缩小 都进行标准化处理 实例化两个标准api

    # 因为两个特征维度不一样不一样，所以实例化两个标准化api
    std_x = StandardScaler()

    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train.reshape(-1,1))
    y_test = std_y.transform(y_test.reshape(-1,1))

    lr = LinearRegression()
    lr.fit(x_train,y_train)

    print(lr.coef_)
    # 保存模型
    joblib.dump(lr,"./tmp/test.pkl")
    model = joblib.load("./tmp/test.pkl")
    print("预测的结果：",std_y.inverse_transform(model.predict(x_test)))

    y_predict = std_y.inverse_transform(lr.predict(x_test))
    print("房子的预测价格：",y_predict)
    print(lr.score(x_test,y_test))

    # 梯度下降
    sgd = SGDRegressor()
    sgd.fit(x_train, y_train)
    print(sgd.coef_)

    sgd_y_predict = std_y.inverse_transform(sgd.predict(x_test))
    print("梯度下降房子的预测价格",sgd_y_predict)
    print(sgd.score(x_test,y_test))

    print("梯度下降的均方误差：",mean_squared_error(std_y.inverse_transform(y_test),sgd_y_predict))

    # 岭回归进行房价预测
    rd = Ridge(alpha=1.0)
    rd.fit(x_train,y_train)
    print(rd.coef_)
    rd_y_predict = std_y.inverse_transform(rd.predict(x_test))
    print("梯度下降房子的预测价格",rd_y_predict)
    print(rd.score(x_test,y_test))
    print("梯度下降的均方误差：",mean_squared_error(std_y.inverse_transform(y_test),rd_y_predict))

二 逻辑回归：

1.应用场景：广告点击率：是否点击

2.公式与线性回归公式一样，但最后要经过一个sigmoid函数进行激活，将得到的值映射成概率，转换成分类问题

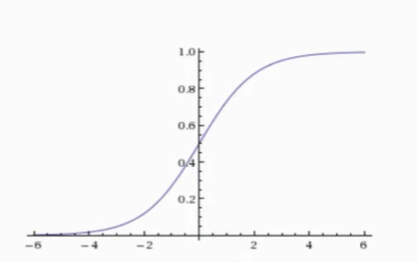
3.激活函数：sigmoid函数：

逻辑回归输入和线性回归一样

sigmod把值映射到0-1之间

4.损失函数：【衡量逻辑回归的策略】

5.问题: 多个局部最小值问题解决：

(1)多次随机初始化，多次比较最小值结果

(2)调整学习率来改善

6.逻辑回归例子：

def logistic():
    ''' 逻辑回归做二分类进行癌症预测(根据细胞的属性特征) :return: '''

    # 读取数据

    column = ['radius','texture','perimeter','area','smoothness','compactness','concavity','concave points','symmetry','fractal dimension','evl']
    data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",names=column)

    data = data.replace(to_replace='?', value=1)

    data = data.dropna()

    print(data)
    x_train,y_train,x_test,y_test = train_test_split(data[column[1:10]],data[column[10]],test_size=0.25)

    # 标准化 分类不用做标准化处理

    std = StandardScaler()

    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)


    lg = LogisticRegression(C=1.0)

    lg.fit(x_train,y_train)

    y_predict = lg.predict(x_test)

    print(y_predict)

    print("得分：",lg.score(x_test,y_test))