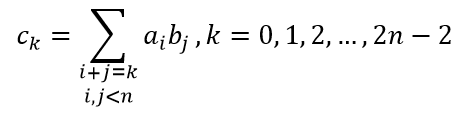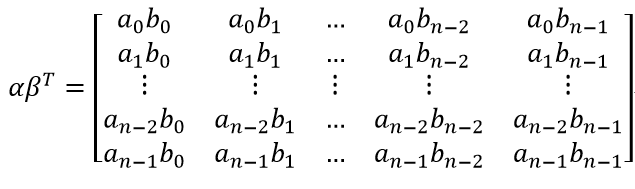大家好，欢迎来到IT知识分享网。

一、conv()的基本使用方法

conv 计算 卷积和多项式乘法
w = conv(u,v) 返回向量 u 和 v 的卷积。如果 u 和 v 是多项式系数的向量，对其卷积与将这两个多项式相乘等效。

w = conv(u,v,shape) 返回如 shape 指定的卷积的分段。例如，conv(u,v,‘same’) 仅返回与 u 等大小的卷积的中心部分，而 conv(u,v,‘valid’) 仅返回计算的没有补零边缘的卷积部分。

示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。

二、conv()使用的一些例子

1.多项式的计算

就是那种正常的多项式运算，通过矩阵表示系数，返回运算结果。
如现在要运算(x+2)*(x+3)，可采用如下代码

u=[1 3];
v=[1 2];%行向量表示
y=conv(u,v)

结果y=[1 5 6]
同样也可以利用这个函数进行更加复杂的运算。

2.向量卷积

创建两个向量并求其卷积。

向量的卷积是什么？？？？

给定两个n维向量α=(a0, a1, …, an-1)T，β=(b0, b1, …, bn-1)T，则α与β的卷积运算定义为：α*β=(c0, c1, …, c2n-2)T，其中

其实向量的卷积也就类似多项式的乘法，这里的话，假定为两个多项式相乘，从行看上去，就是对应的系统，从x的零次方到x的n-1次方。
单单从数学含义上看一种运算方法，下面也来看看这种运算方法得到的结果吧。

u = [1 2 3];
v = [1 2 3];  %其中w的长度是u和v长度相加减1
w = conv(u,v)

w =1 4 10 12 9

总结

两个向量 u 和 v 的卷积，表示 v 滑过 u 时依据这些点确定的重叠部分的面积。从代数方法上讲，卷积是与将其系数为 u 和 v 元素的多项式相乘相同的运算.