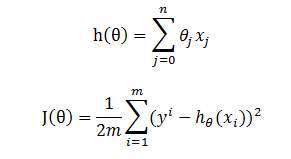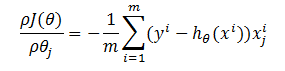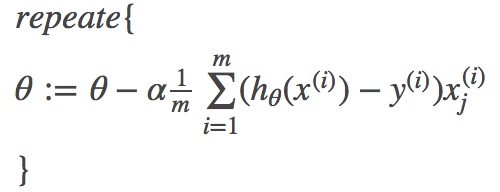梯度下降（详解）

大家好，欢迎来到IT知识分享网。

机器学习中我们经常可以看见梯度下降这个名词，但是什么是梯度下降？梯度下降是用来干什么的？网上一大堆文章，看到最后也没看出个名堂出来，刚好今天看到了篇文章，然后结合自己的一些理解，记录下。

【什么是梯度下降】

首先我们可以把梯度下降拆解为梯度+下降，那么梯度可以理解为导数（对于多维可以理解为偏导），那么合起来变成了：导数下降，那问题来了，导数下降是干什么的？这里我直接给出答案：梯度下降就是用来求某个函数最小值时自变量对应取值

其中这句话中的某个函数是指：损失函数（cost/loss function），直接点就是误差函数。

一个算法不同参数会产生不同拟合曲线，也意味着有不同的误差。

损失函数就是一个自变量为算法的参数，函数值为误差值的函数。所以梯度下降就是找让误差值最小时候算法取的参数。

【补充点小知识】

在机器学习中有一类算法就是产生一条曲线来拟合现有的数据，这样子就可以实现预测未来的数据，我们将这个算法叫做回归。

还有一类算法也是产生一条曲线，但是这条曲线用来将点分为两块，实现分类，我们将这个算法叫做分类。

但是这面两种算法产生的拟合曲线并不是完全和现有的点重合，拟合曲线和真实值之间有一个误差。所以我们一般用损失函数的

值来衡量这个误差，所以损失函数的误差值越小说明拟合效果越好。（简单理解：损失函数表示预测值与实际值之间的误差。）

【梯度为什么要下降】

梯度为什么下降我们可以将它理解为：找误差函数（损失函数）最小值对应的自变量。

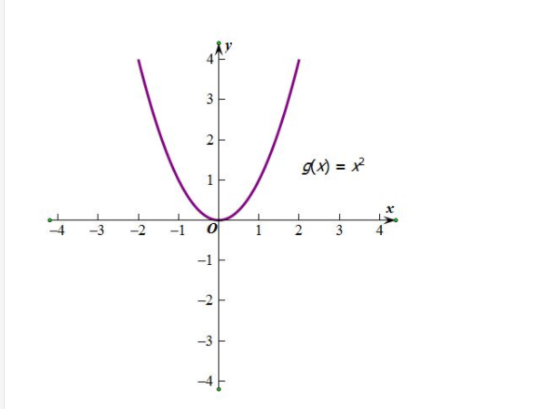
下图所示，这个二次函数对应曲线就是一个误差函数（损失函数），其中自变量是算法的参数，函数值是是该参数下所产生拟合

曲线和真实值之间的误差值。（注意了：一般你看到梯度下降的公式最好想到下面这个图，对就假设误差函数就这么特殊，都是

开口朝上，都是平滑的，都是只有一个导数为0的点，都是弯一下而不是弯很多下。）

【梯度下降是如何做到的】

我们还是以上面那个图为例子，那么要你找最小值对应的自变量x，你怎么找？记住我们目的是为了找自变量x。

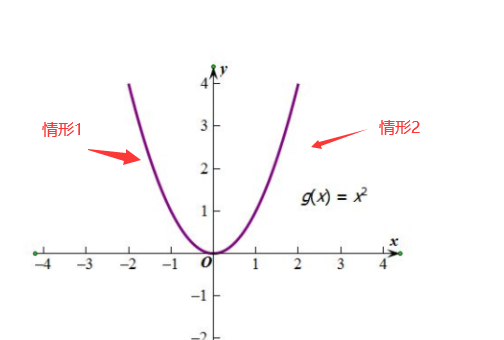
情形1：

单调下降，导数为负（梯度为负），要想找到函数的最小值所对应的自变量的值（曲线最低点对应x的值）

怎么走？

当然是水平向右滑啦，也就是让x增大，此时随着x增大，导数（梯度）的绝对值是减小的（梯度下降含义懂了吧）

情形2：

单调上升，导数为正（梯度为正），要想找到函数的自变量的值（曲线最低点对应x的值）

怎么走？

当然是水平向左滑啦，也就是让x减小，此时随着x减小，导数（梯度）的绝对值是减小的（也就是梯度下降）。

【总结】

梯度下降的含义大概可以理解为：

改变x的值使得导数的绝对值变小，当导数小于0时候（情形1），我们要让目前x值大一点点，再看它导数值。

当导数大于0时候（情形2），我们要让目前x值减小一点点，再看它导数值。

当导数接近0时候，我们就得到想要的自变量x了。也就是说找到这个算法最佳参数，使得拟合曲线与真实值误差最小。

官方点讲大概意思就是：梯度下降就是找让误差值最小时候算法取的参数

参考文章

1.https://www.zhihu.com/question/305638940/answer/670034343

2.https://zhuanlan.zhihu.com/p/43452377

————————————————————————-2020-10-26更新————————————————————————

恩恩，今天在看一下觉得自己上面的那些解释可能太片面了，今天在进一步来阐述下梯度下降。

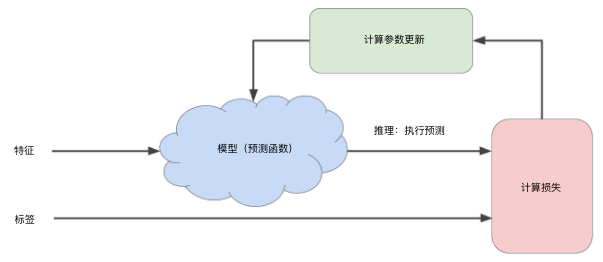
在训练机器学习模型时，首先对权重和偏差进行初始猜测，然后反复调整这些猜测，直到获得损失可能最低的权重和偏差为止（即模型收敛），如下图所示：

而梯度下降是机器学习中最常用的计算代价函数（损失函数）的方法，它只需要计算损失函数的一阶导数。

假设 h(θ) 为目标函数，而 J(θ) 为损失函数，

损失函数的梯度（即偏导数）为

这一步就是将h(θ)带入下面式子，然后求导就可以得到了，这里就不详细解释了。

按参数 θ 的梯度负方向，来更新θ，即梯度下降算法为