大家好,欢迎来到IT知识分享网。
终于AC了一次。。。NOIPAC不易啊。。
1. 潜伏者
(spy.pas/c/cpp)

【问题描述】
R国和S国正陷入战火之中,双方都互派间谍,潜入对方内部,伺机行动。
历经艰险后,潜伏于S国的R国间谍小C终于摸清了S国军用密码的编码规则:
1、S国军方内部欲发送的原信息经过加密后在网络上发送,原信息的内容与加密后所的内容均由大写字母‘A’—‘Z’构成(无空格等其他字母)。
2、S国对于每个字母规定了对应的“密字”。加密的过程就是将原信息中的所有字母替换为其对应的“密字”。
3、每个字母只对应一个唯一的“密字”,不同的字母对应不同的“密字”。“密字”可以和原字母相同。
例如,若规定‘A’的密字为‘A’,‘B’的密字为‘C’(其他字母及密字略),则原信息“ABA”被加密为“ACA”。
现在,小C通过内线掌握了S国网络上发送的一条加密信息及其对应的原信息。小C希望能通过这条信息,破译S国的军用密码。小C的破译过程是这样的:扫描原信息,对于原信息中的字母x(代表任一大写字母),找到其在加密信息中的对应大写字母y,并认为在密码里y是x的密字。如此进行下去直到停止于如下的某个状态:
1、 所有信息扫描完毕,‘A’—‘Z’所有26个字母在原信息中均出现过并获得了相应的“密字”。
2、所有信息扫描完毕,但发现存在某个(或某些)字母在原信息中没有出现。
3、扫描中发现掌握的信息里有明显的自相矛盾或错误(违反S过密码的编码规则)。例如某条信息“XYZ”被翻译为“ABA”就违反了“不同字母对应不同密字”的规则。
在小C忙得头昏脑胀之际,R国司令部又发来电报,要求他翻译另外一条从S国刚刚截取到的加密信息。现在请你帮助小C:通过内线掌握的信息,尝试破译密码。然后利用破译的密码,翻译电报中的加密信息。
【输入】
输入文件名为spy.in,共3行,每行为一个长度在1到100之间的字符串。
第1行为小C掌握的一条加密信息。
第2行为第1行的加密信息所对应的原信息。
第3行为R国司令部要求小C翻译的加密信息。
输入数据保证所有字符串仅由大写字母‘A’—‘Z’构成,且第1行长度与第2行相等。
【输出】
输出文件spy.out共1行。
若破译密码停止时出现2,3两种情况,请你输出“Failed”(不含引号,注意首字母大写,其它小写)。
否则请输出利用密码翻译电报中加密信息后得到的原信息。
【输入输出样例1】
| spy.in | spy.out |
|---|---|
| AA | Failed |
| AB | |
| EOWIE |
【输入输出样例1说明】
原信息中的字母‘A’和‘B’对应相同的密字,输出“Failed”。
【输入输出样例2】
| spy.in | spy.out |
|---|---|
| QWERTYUIOPLKJHGFDSAZXCVBN | Failed |
| ABCDEFGHIJKLMNOPQRSTUVWXY | |
| DSLIEWO |
【输入输出样例2说明】
字母‘Z’在原信息中没有出现,输出“Failed”。
【输入输出样例3】
| spy.in | spy.out |
|---|---|
| MSRTZCJKPFLQYVAWBINXUEDGHOOILSMIJFRCOPPQCEUNYDUMPP | Failed |
| YIZSDWAHLNOVFUCERKJXQMGTBPPKOIYKANZWPLLVWMQJFGQYLL | |
| FLSO |
水题不解释。
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
char ch[26]={
'0'};
int main(){
freopen("spy.in","r",stdin);
freopen("spy.out","w",stdout);
string str1,str2,str3;
cin>>str1>>str2>>str3;
int len1=str1.length(),len3=str3.length();
if(len1<26){
cout<<"Failed";
return 0;
}
for(int i=0;i<len1;i++){
for(int j=0;j<i;j++){
if(str2[i]==str2[j]&&str1[i]!=str1[j]){
cout<<"Failed";
return 0;
}
}
ch[str1[i]-'A']=str2[i];
}
for(int i=0;i<len3;i++)cout<<ch[str3[i]-'A'];
return 0;
}2. Hankson的趣味题
(son.pas/c/cpp)

【问题描述】
Hanks博士是BT(Bio-Tech,生物技术)领域的知名专家,他的儿子名叫Hankson。现在,刚刚放学回家的Hankson正在思考一个有趣的问题。
今天在课堂上,老师讲解了如何求两个正整数c1和c2的最大公约数和最小公倍数。现在Hankson认为自己已经熟练地掌握了这些知识,他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”,这个问题是这样的:已知正整数a0,a1,b0,b1,设某未知正整数x满足:
1、 x和a0的最大公约数是a1;
2、 x和b0的最小公倍数是b1。
Hankson的“逆问题”就是求出满足条件的正整数x。但稍加思索之后,他发现这样的x并不唯一,甚至可能不存在。因此他转而开始考虑如何求解满足条件的x的个数。请你帮助他编程求解这个问题。
【输入】
输入文件名为son.in。第一行为一个正整数n,表示有n组输入数据。接下来的n行每行一组输入数据,为四个正整数a0,a1,b0,b1,每两个整数之间用一个空格隔开。输入数据保证a0能被a1整除,b1能被b0整除。
【输出】
输出文件son.out共n行。每组输入数据的输出结果占一行,为一个整数。
对于每组数据:若不存在这样的x,请输出0;
若存在这样的x,请输出满足条件的x的个数;
【输出输出样例】
| son.in | son.out |
|---|---|
| 2 | 6 |
| 41 1 96 288 | 2 |
| 95 1 37 1776 |
【说明】
第一组输入数据,x可以是9、18、36、72、144、288,共有6个。
第二组输入数据,x可以是48、1776,共有2个。
【数据范围】
对于50%的数据,保证有1≤a0,b1,b0,b1≤10000且n≤100。
对于100%的数据,保证有1≤a0,b1,b0,b1≤2,000,000,000且n≤2000。
题解
对于这道题,暴力搜索其实是可以的。like this。
#include<cstdio>
#include<iostream>
using namespace std;
template<class T>inline void readin(T &res){
static char ch;
while((ch=getchar())<'0'||ch>'9');res=ch-48;
while((ch=getchar())>='0'&&ch<='9')res=ch-48+res*10;
}
int n,a0,a1,b0,b1,ans;
int gcd(int x,int y){
return y==0?x:gcd(y,x%y);
}
int lcm(int x,int y){
return x/gcd(x,y)*y;
}
bool judge(int x){
if(gcd(x,a0)!=a1)return 0;
if(lcm(x,b0)!=b1)return 0;
return 1;
}
int main(){
freopen("son.in","r",stdin);
freopen("son.out","w",stdout);
readin(n);
while(n--){
int ans=0;
readin(a0),readin(a1),readin(b0),readin(b1);
for(int i=1;i*i<=b1;i++){
if(b1%i==0){
if(judge(i))ans++;
if(i*i!=b1)if(judge(b1/i))ans++;
}
}
printf("%d\n",ans);
}
return 0;
}对于2*1e9来说, sqrt(2∗1e9)≈44721 ,所以就可以暴力枚举过掉。
但是很明显的,如果不是质因数的话就不需要判断,所以又我们可以先用素数筛得质因数,然后就可以纵横驰骋了。。。。
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
template<class T>inline void readin(T &res){
static char ch;
while((ch=getchar())<'0'||ch>'9');res=ch-48;
while((ch=getchar())>='0'&&ch<='9')res=ch-48+res*10;
}
int vis[45000],a0,a1,b0,b1,n,tot,prime[45005];//sqrt(2*1e9)=44721
int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
int main(){
freopen("son.in","r",stdin);
freopen("son.out","w",stdout);
readin(n);
for(register int i=2;i<=45000;i++){
//素数筛,在这里有奇效 取sqrt(2*10^9)即可。
if(!vis[i])prime[++tot]=i;
for(register int j=1;j<=tot;j++){
if(i*prime[j]>45000)break;
vis[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}//由于45000太小了,各种筛法在这里其实效率近似。
for(register int i=1;i<=n;i++){
readin(a0),readin(a1),readin(b0),readin(b1);
ll k=b1/b0;
int tmp=b1/b0,a=gcd(k,b0),q=b0/a;
while(a!=1){
k*=(ll)a;
a=gcd(k,q);
q/=a;
}
k=(ll)k/gcd(k,a1)*a1;
if(gcd(k,a0)!=a1)b0=0;
if((ll)b0*tmp%k)b0=0;
else b0=(ll)b0*tmp/k;
if(b0){
int kkk=a0/a1,jl=1,ans=1;
a=gcd(b0,kkk);q=b0/a;
while(a!=1){
jl*=a;
a=gcd(kkk,q);
q/=a;
}
b0/=jl;
if(b0){
for(register int j=1;prime[j]*prime[j]<=b0&&j<=tot;j++){
int cnt=1;
while(!(b0%prime[j])){
b0/=prime[j];
cnt++;
}
ans*=cnt;
}
if(b0!=1)ans*=2;
printf("%d\n",ans);
}else printf("0\n");
}
else printf("0\n");
}
return 0;
}3.最优贸易
(trade.pas/c/cpp)

【问题描述】
C国有n个大城市和m条道路,每条道路连接这n个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这m条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为1条。
C国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到C国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设C国n个城市的标号从1-n,阿龙决定从1号城市出发,并最终在n号城市结束自己的旅行。在旅游的过程中,任何城市可以重复经过多次,但不要求经过所有n个城市。阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市迈入他最喜欢的商品——水晶球,并在之后经过的另一个城市卖出这个水晶球。用赚取的差价当作旅费。由于阿龙主要是来C国旅游,他决定这个贸易只进行最多一次。当然,在赚不到差价的情况下它就无需进行贸易。
假设C国有5个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路为单向通行。双向箭头表示这条道路为双向通行。
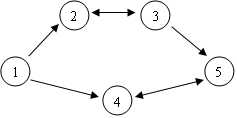
假设1~n号城市的水晶球价格分别为4,3,5,6,1。
阿龙可以选择如下一条线路:1->2->3->5,并在2号城市以3的价格买入水晶球,在3号城市以5的价格卖出水晶球,赚取的旅费数为2。
阿龙也可以选择如下一条线路:1->4->5->4->5,并在第1次到达5号城市时以1的价格买入水晶球,在第2次到达4号城市时以6的价格卖出水晶球,赚取的旅费数为5。
现在给出n个城市的水晶球价格,m条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。请你告诉阿龙,他最多能赚钱多少旅费。
【输入】
输入文件名为trade.in。
第一行包含2个正整数n和m,中间用一个空格隔开,分别表示城市的数目和道路的数目。
第二行n个正整数,每两个正整数之间用一个空格隔开,按标号顺序分别表示这n个城市的商品价格。
接下来m行,每行有3个正整数,x,y,z,每两个整数之间用一个空格隔开。如果z=1,表示这条道路是城市x到城市y之间的单向道路;如果z=2,表示这条道路为城市x和城市y之间的双向道路。
【输出】
输出文件trade.out共1行,包含1个整数,表示最多能赚取的旅费。如果没有进行贸易,则输出0。
【输出输出样例】
| trade.in | trade.out |
|---|---|
| 5 5 | 4 |
| 4 3 5 6 1 | |
| 1 2 1 | |
| 1 4 1 | |
| 2 3 2 | |
| 3 5 1 | |
| 4 5 2 |
【数据范围】
输入数据保证1号城市可以到达n号城市。
对于10%的数据,1≤n≤6。
对于30%的数据,1≤n≤100。
对于50%的数据,不存在一条旅游路线,可以从一个城市出发,再回到这个城市。
对于100%的数据,1≤n≤100000,1≤m≤500000,1≤x,y≤n,1≤z≤2,1≤各城市水晶球价格≤100。
题解
算法一:
结合数据规模。对于30%的数据,可以用另类求最大最小的类似floyed的立方算法解决。对于50%的数据,由题意可知这部分数据死拓扑有序的,直接dp即可。用F表示从第一个点出发到达第i个点用最小钱能买到的水晶球。状态转移方程如下F=min(F[j],A),如果第i个点能到达第N个点,那么用A-F更新答案。这种算法需要结合数据,编程复杂度较大,如果拓扑排序写得较好可以得到超过50分的分数。期望得分(50-80)。就不加code了。
算法二:
求强连通分支后,很显然图仍然是拓扑有序的。用类似的dp解决即可。但是强连通好像是超过联赛大纲的,而且编程复杂度较高,且由于方法十分经典,不再详细介绍。复杂度O(N+M),期望得分100。
#include<algorithm>
#include<vector>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<stack>
#define INF 2100000000
#define ll long long
#define clr(x) memset(x,0,sizeof(x))
#define N 100005
#define M 500005
using namespace std;
//这道题一开始我是用的双向spfa,但是spfa永远大于O(N+M),所以思考数据范围大了以后
//或使用锯型数据后,spfa不适用(但应该还是能卡过),特别是作为稠密图时trajan的效率就可以完美体现。
template<class T>inline void readin(T &res){
static char ch;
while((ch=getchar())<'0'||ch>'9');res=ch-48;
while((ch=getchar())>='0'&&ch<='9')res=ch-48+res*10;
}
int first[N],next[M<<1],to[M<<1],t;// 仍然要有两个图,想想为什么?
int _first[N],_next[M<<1],_to[M<<1],in[N],_t;
void addedge(int s,int v){
next[++t]=first[s];
first[s]=t;
to[t]=v;
}
void linkedge(int s,int v){
_next[++_t]=_first[s];
_first[s]=_t;
_to[_t]=v;
in[v]++;
}
int chuo,low[N],trn[N],vis[N],belong[N],st;
int sta[N],tail,_sta[N];
int a[N],mi[N],mx[N],fi[N],fx[N],m,n;
void tarjan(int x){
//核心处理,trajan的优秀效果就不用我多说了吧
trn[x]=low[x]=++chuo;
vis[x]=1;
_sta[x]=1;
sta[++tail]=x;
for(register int i=first[x];i;i=next[i]){
int v=to[i];
if(vis[v]&&_sta[v])low[x]=min(low[x],trn[v]);
else if(!vis[v]){
tarjan(v);
low[x]=min(low[x],low[v]);
}
}
if(trn[x]==low[x]){
st++;
fi[st]=mx[st]=mi[st]=a[x];
while(sta[tail]!=x){
int v=sta[tail--];
belong[v]=st;
_sta[v]=0;
mx[st]=max(mx[st],a[v]);
fi[st]=mi[st]=min(mi[st],a[v]);
}
_sta[x]=0;
belong[x]=st;
tail--;
}
}
queue<int>Q;
int tp[M],k;
void tuopu(){
//top在这里是为了判断因缩点判断从u到v是否合法。
for(register int i=1;i<=st;i++)
if(!in[i]){
Q.push(i);
tp[++k]=i;
}
while(!Q.empty()){
int s=Q.front();Q.pop();
for(register int i=_first[s];i;i=_next[i]){
int v=_to[i];
in[v]--;
if(in[v]==0){
Q.push(v);
tp[++k]=v;
}
}
}
}
int main(){
freopen("trade.in","r",stdin);
freopen("trade.out","w",stdout);
readin(n),readin(m);
for(register int i=1;i<=n;i++)readin(a[i]);
for(register int i=1;i<=m;i++){
//init()
int x,y,z;
readin(x),readin(y),readin(z);
addedge(x,y);
if(z==2)addedge(y,x);
}
tarjan(1);//缩图,如果我能在一个环内找到一个point,那么这个环内如果确定一个点,后继点就一定能供我选择trade
for(register int i=1;i<=n;i++)
for(register int j=first[i];j;j=next[j])
if(belong[i]!=belong[to[j]])
linkedge(belong[i],belong[to[j]]);
tuopu();
for(register int i=1;i<=k;i++)
for(register int j=_first[tp[i]];j;j=_next[j]){
int v=_to[j];
fi[v]=min(fi[v],fi[tp[i]]);
fx[v]=max(max(fx[v],fx[tp[i]]),mx[v]-fi[v]);
}
cout<<fx[belong[n]];//说到底,这道题的核心并不是所谓的双向spfa或者trajan,只是一道图上dp。trajan或者spfa只是一种实现DAG或最短路的方式。
return 0;
}算法三:
用另类spfa(即求出最大最小值),求出从第一个点出发到其他点能买到水晶球的最小代价。将所有边反向以后,从N点出发求出第N个点到第i个点能卖出水晶球的最大代价,这个代价对应于原图中第i个点到第N个点能获得的最大收益。对于每个点,用最大收益-最小代价更新答案即可。复杂度不好估计,不过稀疏图spfa的效率是很有保证的,且编程复杂度较小,是一种比较优秀的算法。期望得分100。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<stack>
#define rez(i,x,y) for(int i=x;i>=y;i--)
#define res(i,x,y) for(int i=x;i<=y;i++)
#define INF 210000
#define ll long long
#define N 100001
#define clr(x) memset(x,0,sizeof(x))
#define NAME "trade"
//宁死,也不打链式前向新!!!!
//真心不想打邻接链表啊!!!!!
using namespace std;
vector<int> first[N];
vector<int> second[N];
int n,m,ans;
int v[N],mfirst[N],temp[N],msecond[N];
//以前的AC代码
void spfa_first(){
queue<int> q;
q.push(1);
temp[1]=1;mfirst[1]=v[1];
while(!q.empty()){
int u=q.front();
for(int i=0;i<first[u].size();i++){
int t=first[u][i];
if(!mfirst[t])mfirst[t]=v[t];
mfirst[t]=min(mfirst[t],mfirst[u]);
if(!temp[t]){
q.push(t);
temp[t]=1;
}
}
q.pop();
}
}
void spfa_second(){
clr(temp);
queue<int> q;
q.push(n);
temp[n]=1;msecond[n]=v[n];
while(!q.empty()){
int u=q.front();
for(int i=0;i<second[u].size();i++){
int t=second[u][i];
if(!msecond[t])msecond[t]=v[t];
msecond[t]=max(msecond[t],msecond[u]);
if(!temp[t]){
q.push(t);
temp[t]=1;
}
}
q.pop();
}
}
int main(){
freopen(NAME".in","r",stdin);
freopen(NAME".out","w",stdout);
cin>>n>>m;
for(int i=1;i<=n;i++){
scanf("%d",&v[i]);
}
for(int x,y,z,i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
first[x].push_back(y);
second[y].push_back(x);
if(z>1){
first[y].push_back(x);
second[x].push_back(y);
}
}
spfa_first();
spfa_second();
for(int i=1;i<=n;i++)ans=max(msecond[i]-mfirst[i],ans);
cout<<ans;
return 0;
}靶形数独

【问题描述】
小城和小华都是热爱数学的好学生,最近,他们不约而同地迷上了数独游戏,好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了,于是他们向Z博士请教,Z博士拿出了他最近发明的“靶形数独”,作为这两个孩子比试的题目。
靶形数独的方格同普通数独一样,在9格宽×9格高的大九宫格中有9个3格宽×3格高的小九宫格(用粗黑色线隔开的)。在这个大九宫格中,有一些数字是已知的,根据这些数字,利用逻辑推理,在其他的空格上填入1到9的数字。每个数字在每个小九宫格内不能重复出现,每个数字在每行、每列也不能重复出现。但靶形数独有一点和普通数独不同,即每一个方格都有一个分值,而且如同一个靶子一样,离中心越近则分值越高。(如图)
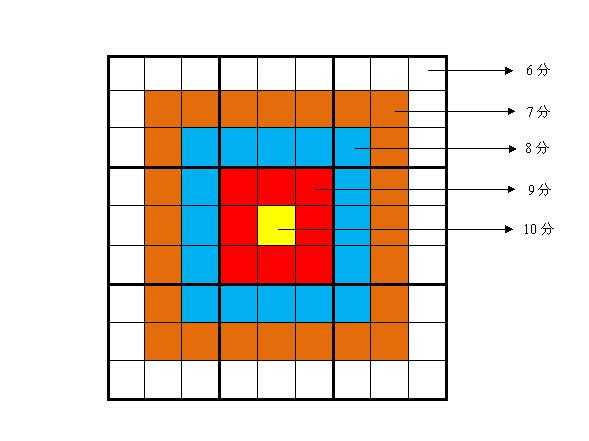
上图具体的分值分布是:最里面一格(黄色区域)为10分,黄色区域外面的一圈(红色区域)每个格子为9分,再外面一圈(蓝色区域)每个格子为8分,蓝色区域外面一圈(棕色区域)每个格子为7分,最外面一圈(白色区域)每个格子为6分,如上图所示。比赛的要求是:每个人必须完成一个给定的数独(每个给定数独有可能有不同的填法),而且要争取更高的总分数。而这个总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。如图,在以下这个已经填完数字的靶形数独游戏中,总分为2829。游戏规定,将以总分数的高低决出胜负。
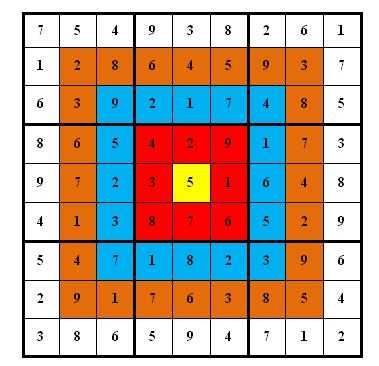
由于求胜心切,小城找到了善于编程的你,让你帮他求出,对于给定的靶形数独,能够得到的最高分数。
【输入】
输入文件名为sudoku.in。
一共9行,每行9个整数(每个数都在0—9的范围内),表示一个尚未填满的数独方格,未填满的空格用“0”表示。每两个数字之间用一个空格隔开。
【输出】
输出文件sudoku.out共1行。
输出可以得到的靶形数独的最高分数。如果这个数独无解,则输出整数-1。
【输入输出样例1】
| sudoku.in | sudoku.in |
|---|---|
| 7 0 0 9 0 0 0 0 1 | 2829 |
| 1 0 0 0 0 5 9 0 0 | |
| 0 0 0 2 0 0 0 8 0 | |
| 0 0 5 0 2 0 0 0 3 | |
| 0 0 0 0 0 0 6 4 8 | |
| 4 1 3 0 0 0 0 0 0 | |
| 0 0 7 0 0 2 0 9 0 | |
| 2 0 1 0 6 0 8 0 4 | |
| 0 8 0 5 0 4 0 1 2 |
【输入输出样例2】
| sudoku.in | sudoku.in |
|---|---|
| 0 0 0 7 0 2 4 5 3 | 2852 |
| 9 0 0 0 0 8 0 0 0 | |
| 7 4 0 0 0 5 0 1 0 | |
| 1 9 5 0 8 0 0 0 0 | |
| 0 7 0 0 0 0 0 2 5 | |
| 0 3 0 5 7 9 1 0 8 | |
| 0 0 0 6 0 1 0 0 0 | |
| 0 6 0 9 0 0 0 0 1 | |
| 0 0 0 0 0 0 0 0 6 |
【数据范围】
40%的数据,数独中非0数的个数不少于30。
80%的数据,数独中非0数的个数不少于26。
100%的数据,数独中非0数的个数不少于24。
第三遍做这道题了,加了许许多多优化,比std快5倍左右。
就是普普通通的位运算,这道题是熟练掌握位运算的一道好题。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<stack>
#define rez(i,x,y) for(int i=x;i>=y;i--)
#define res(i,x,y) for(int i=x;i<=y;i++)
#define INF 2100000000
#define ll long long
#define clr(x) memset(x,0,sizeof(x))
#define erk(i) (1<<(i))
#define ider(i,j) ((i)/3*3+(j)/3)
#define order(i,j) (3*((i)-(i)/3*3)+(j)-(j)/3*3)
using namespace std;
//相信自己位运算比dancing link快。(然而并不是。。)
int mp[11][11],row[9],lie[9],line[9],ninebox[9],t=0,tot=0;//lie就是列,line是行,ninebox是九宫格,row是依据你选择的主要决定方式而定
int wys[512],node[9],cnt[9],fin,ans;
int sore[9][9]={
{
6,6,6,6, 6,6,6,6,6},
{
6,7,7,7, 7,7,7,7,6},
{
6,7,8,8, 8,8,8,7,6},
{
6,7,8,9, 9,9,8,7,6},
{
6,7,8,9,10,9,8,7,6},
{
6,7,8,9, 9,9,8,7,6},
{
6,7,8,8, 8,8,8,7,6},
{
6,7,7,7, 7,7,7,7,6},
{
6,6,6,6, 6,6,6,6,6}};
void SUM(){
//计算数值
int tmp=0;
for(int i=0;i<9;i++)
for(int j=0;j<9;j++)
tmp+=mp[i][j]*sore[i][j];
if(ans<tmp)ans=tmp;
}
void dfs(int ti){
int i,j,p;
int pos,k;
if(ti==9){
//一种情况的完结
SUM();return;
}
i=node[ti];
if(cnt[i]==0){
//此层已处理完毕
dfs(ti+1);return;
}
cnt[i]--;
p=511^row[i];p=p&-p;//得到未处理的位置信息
row[i]|=p;j=wys[p];
pos=511^(lie[i]|line[j]|ninebox[ider(i, j)]);//这道题的精髓,快速判断可填情况
while(pos>0){
k=pos&-pos;pos^=k;
mp[i][j]=wys[k]+1;//给予一种情况
lie[i]|=k;line[j]|=k;//计算当前情况
ninebox[ider(i,j)]|=k;
dfs(ti);
lie[i]^=k;line[j]^=k;//updata
ninebox[ider(i,j)]^=k;
}
cnt[i]++;//还原
row[i]^=p;
}
int main(){
freopen("sudoku.in","r",stdin);
freopen("sudoku.out","w",stdout);
for(register int i=1,j=0;i<=511;i<<=1,j++)wys[i]=j;
for(register int i=0;i<9;i++)//这道题我是以line为基本位置来判断,所以cnt指向line
for(register int j=0;j<9;j++){
cin>>mp[i][j];
if(mp[i][j]!=0){
//输入的是一个限制
row[i]|=erk(j);//这一行的已有位置记录在row中
t=erk(mp[i][j]-1);
if(((lie[i]&t)!=0)||((line[j]&t)!=0)||((ninebox[ider(i,j)]&t)!=0)){
//数独无解
cout<<-1<<endl;return 0;
}
lie[i]|=t;line[j]|=t;//从三方面储存这个数
ninebox[ider(i,j)]|=t;
}else cnt[i]++;//empty line
}
for(register int i=0;i<9;i++)node[i]=i;//对于每一个横、纵、九宫格的可用数的判断
for(register int i=0;i<9;i++)//N^2
for(register int j=i+1;j<9;j++)
if(cnt[node[i]]>cnt[node[j]]){
node[i]^=node[j];//看起来很玄学,通过容斥原理我们可以知道这就是一个swap
node[j]^=node[i];
node[i]^=node[j];
}
while(cnt[node[tot]]==0)tot++;//都看得懂
dfs(tot);//核心
if(ans==0)cout<<-1<<endl;
else cout<<ans<<endl;
return 0;
}
//这道题的关键点在于一次性找到可填的(也就是限定较多的)位置进行填写,然而一
//直用for一定会TLE,反观,假设我们已经知道了部分内容,我们可以判段的方式是
//横向,纵向,九宫格三者合一,可以想到位运算的急速处理可以使我们瞬间知道某一
//位置的信息,从而来dfs。接下来是这次的NEW环节——dancing link!!!
这是一喜欢DLK的闷骚货的DLK
code
//DLX
#include <iostream>
#include <climits>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 1000
#define MAXNODE 10000
#define MAXR 1000
#define FOR(i,A,s) for(register int i=A[s]; i!=s; i=A[i])
#define SLOT 0
#define ROW 1
#define COL 2
#define SUB 3
using namespace std;
int value[10][10] = {
{
0},
{
0, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{
0, 6, 7, 7, 7, 7, 7, 7, 7, 6},
{
0, 6, 7, 8, 8, 8, 8, 8, 7, 6},
{
0, 6, 7, 8, 9, 9, 9, 8, 7, 6},
{
0, 6, 7, 8, 9, 10,9, 8, 7 ,6},
{
0, 6, 7, 8, 9, 9, 9, 8, 7, 6},
{
0, 6, 7, 8, 8, 8, 8, 8, 7, 6},
{
0, 6, 7, 7, 7, 7, 7, 7, 7, 6},
{
0, 6, 6, 6, 6, 6, 6, 6, 6, 6}
};
inline int encode(int a,int b,int c){
return a*81+b*9+c+1;
}
inline void decode(int code,int &a,int &b,int &c){
code--;
c=code%9; code/=9;
b=code%9; code/=9;
a=code;
}
struct DLX{
int n,sz;
int S[MAXN];
int row[MAXNODE],col[MAXNODE];
int L[MAXNODE],R[MAXNODE],U[MAXNODE],D[MAXNODE];
int ansd,ans[MAXR],ansf;
void init(int n){
//n为列数
this->n=n;
ansf=0;
for(int i=0; i<=n; i++){
U[i]=i; D[i]=i;
L[i]=i-1; R[i]=i+1;
}
L[0]=n; R[n]=0;
sz=n+1;
memset(S,0,sizeof(S));
}
void addRow(int r,int n,int columns[]){
int first=sz;
for(int i=0; i<n; i++){
int &c=columns[i];
L[sz]=sz-1; R[sz]=sz+1;
D[sz]=c; U[sz]=U[c];
D[U[c]]=sz; U[c]=sz;
row[sz]=r; col[sz]=c;
S[c]++;
sz++;
}
R[sz-1]=first; L[first]=sz-1;
}
void remove(int c){
L[R[c]]=L[c];
R[L[c]]=R[c];
FOR(i,D,c)
FOR(j,R,i){
U[D[j]]=U[j];
D[U[j]]=D[j];
--S[col[j]];
}
}
void restore(int c){
FOR(i,U,c)
FOR(j,L,i){
++S[col[j]];
U[D[j]]=j;
D[U[j]]=j;
}
L[R[c]]=c;
R[L[c]]=c;
}
bool dfs(int d){
if (R[0]==0){
int t=0;
for(register int i=0; i<d; i++){
int r,c,v;
decode(ans[i],r,c,v);
t+=value[r+1][c+1]*(v+1);
}
ansf=max(ansf,t);
return true;
}
int c=R[0];
FOR(i,R,0) if (S[i]<S[c]) c=i;
remove(c);
bool flag=false;
FOR(i,D,c){
ans[d]=row[i];
FOR(j,R,i) remove(col[j]);
bool x=dfs(d+1);
flag=flag||x;
FOR(j,L,i) restore(col[j]);
}
restore(c);
return flag;
}
};
DLX solver;
int puzzle[16][20];
int main(){
for(register int i=0; i<9; i++){
for(register int j=0; j<9; j++){
cin>>puzzle[i][j];
puzzle[i][j]--;
}
}
solver.init(9*9*4);
for(register int r=0; r<9; r++){
for(register int c=0; c<9; c++){
for(register int v=0; v<9; v++){
if (puzzle[r][c]==-1 || puzzle[r][c]==v){
int columns[5];
columns[0]=encode(SLOT,r,c);
columns[1]=encode(ROW,r,v);
columns[2]=encode(COL,c,v);
columns[3]=encode(SUB,(r/3)*3+c/3,v);
solver.addRow(encode(r,c,v),4,columns);
}
}
}
}
if (!solver.dfs(0)){
cout<<-1<<endl;
return 0;
}
cout<<solver.ansf<<endl;
return 0;
}发一发对比结果吧。。。
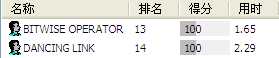
可以看到所谓的dancing link其实并没有想象中的那么神。。。。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/22399.html

