大家好,欢迎来到IT知识分享网。
目 录
1. 一元线性回归模型的数学形式
2. 回归参数β0 , β1的估计
3. 最小二乘估计的性质
线性性
无偏性
最小方差性
一、一元线性回归模型的数学形式
一元线性回归是描述两个变量之间相关关系的最简单的回归模型。自变量与因变量间的线性关系的数学结构通常用式(1)的形式:
y = β0 + β1x + ε (1)
其中两个变量y与x之间的关系用两部分描述。一部分是由于x的变化引起y线性变化的部分,即β0 + β1x,另一部分是由其他一切随机因素引起的,记为ε。该式确切的表达了变量x与y之间密切关系,但密切的程度又没有到x唯一确定y的这种特殊关系。
式(1)称为变量y对x的一元线性回归理论模型。一般称y为被解释变量(因变量),x为解释变量(自变量),β0和β1是未知参数,成β0为回归常数,β1为回归系数。ε表示其他随机因素的影响。一般假定ε是不可观测的随机误差,它是一个随机变量,通常假定ε满足:
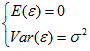
对式(1)两边求期望,得
E(y) = β0 + β1x, (3)
称式(3)为回归方程。
E(ε) = 0 可以理解为 ε 对 y 的总体影响期望为 0,也就是说在给定 x 下,由x确定的线性部分 β0 + β1x 已经确定,现在只有 ε 对 y 产生影响,在 x = x0, ε = 0即除x以外其他一切因素对 y 的影响为0时,设 y = y0,经过多次采样,y 的值在 y0 上下波动(因为采样中 ε 不恒等于0),若 E(ε) = 0 则说明综合多次采样的结果, ε 对 y 的综合影响为0,则可以很好的分析 x 对 y 的影响(因为其他一切因素的综合影响为0,但要保证样本量不能太少);若 E(ε) = c ≠ 0,即 ε 对 y 的综合影响是一个不为0的常数,则E(y) = β0 + β1x + E(ε),那么 E(ε) 这个常数可以直接被 β0 捕获,从而变为公式(3);若 E(ε) = 变量,则说明 ε 在不同的 x 下对 y 的影响不同,那么说明存在其他变量也对 y 有显著作用。
Var(ε) = σ2:因为所有的样本点并不是完全在回归直线上(即 x 与 y 的关系不是确定的函数关系),所以 ε 的方差一定不为0,Var(ε) = σ2的意义为在不同 x 下, ε 对 y 产生同样的波动,是为了后续计算方便,若 ε 的方差对 y 产生的波动随 x 变化,那么需要分析这种变化及其产生的一系列问题。
一般情况下,对所研究的某个实际问题,获得n组样本观测值(x1, y1),(x2, y2),…,(xn, yn),如果它们符合模型(1),则
yi = β0 + β1xi + εi, i = 1, 2, …, n (4)
由式(2)有
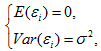
通常还假定n组数据是独立观测的,因而y1,y2,…,yn与ε1,ε2,…,εn都是相互独立的随机变量,而xi(i = 1, 2, …, n)是确定性变量,其值是可以精确测量和控制的。称式(4)为一元线性回归模型。
对式(4)两边分别求数学期望和方差,得
E(yi) = β0 + β1xi, Var(yi) = σ2, i = 1, 2, …, n (6)
可知
个人理解,εi 并不是同分布,因为并不知道他们服从什么分布,从期望和方差相等推不出同分布,虽然同分布下期望和方差一定相等。
E(yi) = β0 + β1xi 从平均意义上表达了变量y与x的统计规律性。在应用上,人们经常关系的正是这个平均值。
在实际问题中,为了方便对参数β0,β1作区间估计和假设检验,还假定模型(1)中误差项ε遵从正态分布,即
ε ~ N(0,σ2), (7)
(才会满足 εi 同分布)
由于 ε1,ε2,…,εn 是 ε 的独立同分布的样本,因而有
εi ~ N(0,σ2), i = 1, 2, …, n (8)
在εi 遵从正态分布的假定下,进一步有随机变量y,也遵从正态分布
yi ~ N(β0 + β1xi, σ2), i = 1, 2, …, n (9)
二、回归参数β0 , β1的估计
普通最小二乘估计(ordinary least squares estimate, OLSE)
为了得到回归系数的理想估计值,使用OLSE(因为OLSE和方差都是差方和的形式)。对每一个样本观测值(xi, yi),最小二乘法考虑观测值yi与其回归值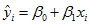
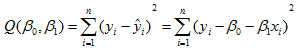
可以看到其回归值是期望值,这里使用到条件 E(ε) = 0.
最小二乘法,就是寻找参数β0,β1的估计值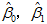
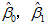
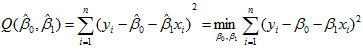
依照式(11)求出的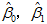
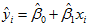
为yi(i = 1, 2,…,n)的回归拟合值,简称回归值或拟合值。称
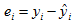
为yi(i = 1, 2, …, n)的残差。
离差和残差:
在本文中离差和残差的公式都是真实值与估计值之间的差,但是,离差是在回归方程得到之前定义的,不能直接得到,通过离差平方和最小来求得回归系数从而得到回归方程,可以将离差看作是风险程度,使离差平方和最小即为使总风险最小。残差是在回归方程得到后定义的,可以直接得到具体数值,若没有回归方程就不存在残差的概念,残差平方和度量了n个样本点观测值到回归直线的距离大小,可以视为随机误差的效应。残差用于研究模型的适用性,也是探测是否违背基本假设的评测量之一。
从式(11)中求出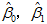
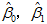
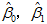
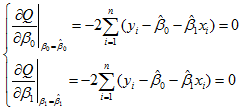
求解正规方程组(14)得β0,β1的最小二乘估计(OLSE)为
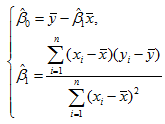
其中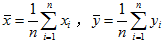
记
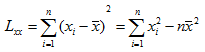
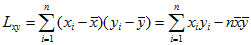
则式(15)可简写为
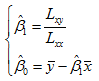
可知
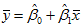
可见回归直线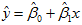
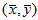
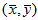
回归直线过点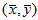
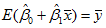
由式(14)可以推出
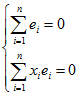
说明残差的均值为0,并且残差以自变量x的加权平均值为0.
三、最小二乘估计的性质
一、线性性
估计量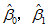
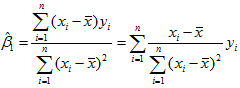
其中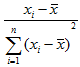
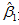
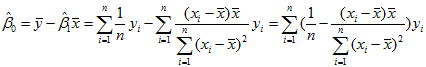
二、无偏性
E(yi) = β0 + β1xi (22)
再由式(18)可得
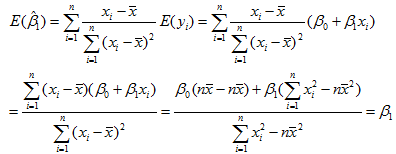
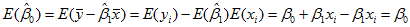
无偏估计的意义是:如果屡次变更数据,反复求β0,β1的估计值,这两个估计量没有高估或低估的系统趋向,它们的平均值将趋向于β0,β1,进一步有
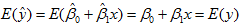
这表明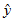
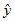
三、最小方差性(最优性、有效性)
方差用来评估变量的波动状况。由y1,y2,..,yn相互独立,Var(yi) = σ2及式(25)得
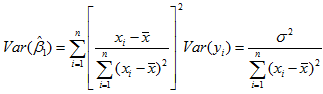
方差的大小表示随机变量取值波动的大小。假设反复抽取容量为n的样本建立回归方程,每次计算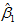
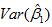
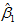
从式(26)可以看到,回归系数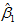
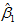
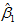
类似地,有
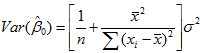
由式(27)可知,回归常数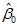
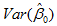
所以从式(26)和(27)可以看出,方差的意义可以用来指导抽样。想要是β0,β1的估计量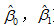
因为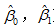
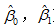
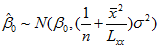
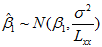
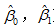
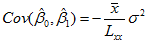
式(30)说明,在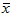
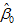
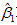
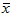
之前给出的回归模型随机误差项εi 等方差及不相关的假定条件,这个条件称为Gauss-Markov条件,即
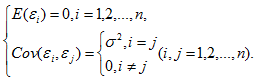
在此条件下可以证明,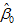
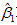
进一步,对于固定的x0,有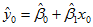
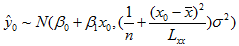
即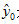
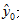
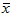
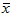
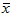
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/27879.html

