小波变换对图像的分解与重构（含matlab代码）

大家好，欢迎来到IT知识分享网。

                                                                           01 小波变换原理  

所谓的小波的小是针对傅里叶波而言，傅里叶波指的是在时域空间无穷震荡的正弦（或余弦波）。

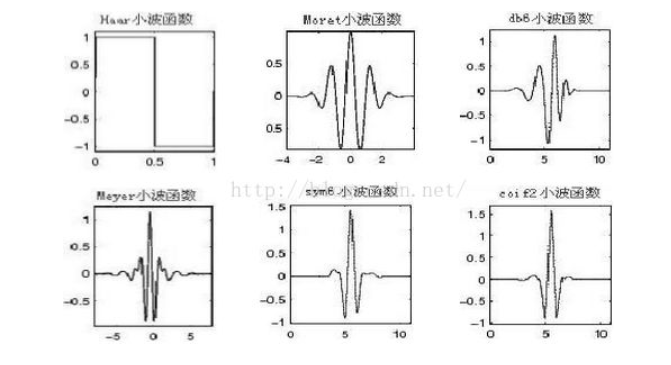
相对而言，小波指的是一种能量在时域非常集中的波，它的能量有限，都集中在某一点附近，而且积分的值为零，这说明它与傅里叶波一样是正交波。举一些小波的例子：

可以看到，能量集中在x轴0值附近，以y轴的0值为基线，上下两个区域的波形面积相等。

众所周知，图像的傅里叶变换是将图像信号分解为各种不同频率的正弦波。同样，小波变换是将图像信号分解为由原始小波位移和缩放之后的一组小波。

小波在图像处理里被称为图像显微镜，原因在于它的多分辨率分解能力可以将图片信息一层一层分解剥离开来。剥离的手段就是通过低通和高通滤波器，

这里我们以一个图像的横向一维为例，讲讲小波的分解与还原，采用的是Haar小波做分解：

图像原始像素矩阵：[6 4 8 7 5 9 3 2]

分解低通滤波器：[ 1  1]/sqrt(2)

分解高通滤波器：[-1 1]/sqrt(2)

1. 用低通滤波器与原始像素矩阵做卷积得：[8 10 12 15 12 14 12 5]/sqrt(2)

下采样得：[10 15 14 5]/sqrt(2)    —–>L

2. 用高通滤波器与原始像素矩阵做卷积得：[-4 2 -4 1 2 -4 6 1]/sqrt(2)

下采样得：[2 1 -4 1]/sqrt(2)    —–>H

上例为一维情况，二维情况在做完横向滤波之后再进行纵向滤波即可。

逆变换过程：

重构低通滤波器：[1  1]/sqrt(2)

重构高通滤波器：[1 -1]/sqrt(2)

1. 对L数组插值得：[0 10 0 15 0 14 0 5]/sqrt(2)

再用低通滤波器做卷积得：[10 10 15 15 14 14 5 5]/2

2. 对H数组插值得：[0 2 0 1 0 -4 0 1]/sqrt(2)

再用高通滤波器做卷积得：[2 -2 1 -1 -4 4 1 -1]/2

两个数组求和得：[6 4 8 7 5 9 3 2] ，矩阵被还原了。

二维图像信号

对于二维图像信号，可以用分别在水平和垂直方向进行滤波的方法实现二维小波多分辨率分解。图2.5为经过二维离散小波变换的分解后子图像的划分。其中:

(l) LL子带是由两个方向利用低通小波滤波器卷积后产生的小波系数，它是图像的近似表示。

(2) HL子带是在行方向利用低通小波滤波器卷积后，再用高通小波滤波器在列方向卷积而产生的小波系数，它表示图像的水平方向奇异特性。（水平子带）

(3) LH子带是在行方向利用高通小波滤波器卷积后，再用低通小波滤波器在列方向卷积而产生的小波系数，它表示图像的垂直方向奇异特性。（垂直子带）

(4) HH子带是由两个方向利用高通小波滤波器卷积后产生的小波系数，它表示图像的对角边缘特性。（对角子带）

 （第一个字母表示列方向的处理，第二个字母表示行方向的处理，图像的奇异特性通过低通时保留，通过高通时被滤除）

小波去噪方法也就是寻找从实际信号空间到小波函数空间的最佳映像，以便得到原信号的最佳恢复。

目前，小波去噪的方法大概可以分为三大类:

第一类方法（小波变换模极大值去噪法）是利用小波变换模极大值原理去噪，即根据信号和噪声在小波变换各尺度上的不同传播特性，剔除由噪声产生的模极大值点，保留信号所对应的模极大值点，然后利用所余模极大值点重构小波系数，进而恢复信号;

第二类方法（小波系数相关性去噪法）是对含噪信号作小波变换之后，计算相邻尺度间小波系数的相关性，根据相关性的大小区别小波系数的类型，从而进行取舍，然后直接重构信号;

第三类方法（小波变换阈值去造法）是小波阈值去噪方法，该方法认为信号对应的小波系数包含有信号的重要信息，其幅值较大，但数目较少，而噪声对应的小波系数是一致分布的，个数较多，但幅值小。

这里主要主要小波阀值收缩去噪法:

小波阀值去噪的基本思想:Donoho提出的小波阀值去噪的基本思想是将信号通过小波变换（采用Mallat算法）后，信号产生的小波系数含有信号的重要信息，将信号经小波分解后小波系数较大，噪声的小波系数较小，并且噪声的小波系数要小于信号的小波系数，通过选取一个合适的阀值，大于阀值的小波系数被认为是有信号产生的，应予以保留，小于阀值的则认为是噪声产生的，置为零从而达到去噪的目的。其基本步骤为：

（1）分解：选定一种层数为N的小波对信号进行小波分解；

（2）阀值处理过程：分解后通过选取一合适的阀值，用阀值函数对各层系数进行量化；

（3）重构：用处理后的系数重构信号。

                                                   02 小波阀值去噪的基本问题

小波阀值去噪的基本问题包括三个方面：小波基的选择，阀值的选择，阀值函数的选择。

（1）小波基的选择：通常我们希望所选取的小波满足以下条件：正交性、高消失矩、紧支性、对称性或反对称性。但事实上具有上述性质的小波是不可能存在的，因为小波是对称或反对称的只有Haar小波，并且高消失矩与紧支性是一对矛盾，所以在应用的时候一般选取具有紧支的小波以及根据信号的特征来选取较为合适的小波。

（2）阀值的选择：直接影响去噪效果的一个重要因素就是阀值的选取，不同的阀值选取将有不同的去噪效果。目前主要有通用阀值（VisuShrink）、SureShrink阀值、Minimax阀值、BayesShrink阀值等。

（3）阀值函数的选择：阀值函数是修正小波系数的规则，不同的反之函数体现了不同的处理小波系数的策略。最常用的阀值函数有两种：一种是硬阀值函数，另一种是软阀值函数。还有一种介于软、硬阀值函数之间的Garrote函数。

另外，对于去噪效果好坏的评价，常用信号的信噪比（SNR）与估计信号同原始信号的均方根误差（RMSE）来判断。

附小波分解与重构图像的matlab程序

clc;
clear;
% 装载图像
load woman;
% X包含载入的图像
% 绘制原始图像
figure(1);
subplot(2,2,1);
image(X);
colormap(map);
title('原始图像');
% 使用sym5对X进行尺度为2的分解
[c,s] = wavedec2(X,1,'sym5');
% 从小波分解结构[c,s]进行尺度为1和2时的低频重构
a1 = wrcoef2('a',c,s,'sym5',1); 
a2 = wrcoef2('a',c,s,'sym5',1); 

% 绘制尺度为1时的低频图像
subplot(2,2,3);
image(a1);colormap(map);
title('尺度为1时的低频图像');
% 绘制尺度为2时的低频图像
subplot(2,2,4);
image(a2);colormap(map);
title('尺度为2时的低频图像');
% 从小波分解结构[c,s]在尺度为2时重构高频
% 'h' 是水平方向
% 'v' 是垂直方向
% 'd' 是对角方向
hd2 = wrcoef2('h',c,s,'sym5',1); 
vd2 = wrcoef2('v',c,s,'sym5',1); 
dd2 = wrcoef2('d',c,s,'sym5',1);
% 绘制高频图像
figure(2);
subplot(2,2,1);
image(hd2);colormap(map);
title('尺度为2时的水平高频图像');
subplot(2,2,2);
image(vd2);colormap(map);
title('尺度为2时的垂直高频图像');
subplot(2,2,3);
image(dd2);colormap(map);
title('尺度为2时的对角高频图像');
subplot(2,2,4);
image(hd2+dd2+vd2+a1);colormap(map);
% 验证这些图像的长度都是sX
sX = size(X)
sa1 = size(a1)
shd2 = size(hd2)
norm(hd2+dd2+vd2+a1-X)