使用cohen kappa系数衡量分类精度

大家好，欢迎来到IT知识分享网。

在诊断试验中，研究者希望考察不同诊断方法在诊断结果上是否具有一致性。如评价两个医务工作者对同一组病人的诊断结论的一致性、同一医务工作者对同一组病人前后进行两次观察作出诊断的一致性。1960年Cohen等提出用Kappa值作为评价判断的一致性程度的指标。实践证明，它是一个描述诊断的一致性较为理想的指标，因此在临床试验中得到广泛的应用。下文给出的例子也都是基于医疗诊断的，可见其提出背景。除此之外，kappa系数也可用于衡量分类精度，在kaggle竞赛中经常被用作评价指标，如2019 data science bowl和PetFinder.my Adoption Prediction等等。

由于诊断试验一致性的大小不完全取决于研究者的临床经验和诊断能力，还可能是由于机遇因素的作用，致使不同研究者得出相同的诊断结论。即没有受过专业医疗教育的人对患者进行诊断也可能会得出与专业医生一样的结论，而这种一致性结论完全是由于机遇因素导致的。kappa系数即是在一致性判断中剔除机遇因素的影响。kappa取值为[0,1]，值越大代表一致性越强/分类精度越高。

kappa系数的计算分为以下几类，下面将通过例子介绍这几种kappa系数如何计算。

简单kappa(simple kappa)
加权kappa(weighted kappa)
- 线性加权(linear weighted kappa)
- 平方加权(quadratic weighted kappa)

Simple Kappa

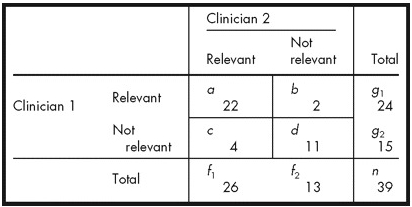
simple kappa的计算公式如下：

$k=\frac{p_{o}-p_{e}}{1-p_{e}}$

其中， $p_{o}$ 代表观察符合率，计算方法为用每一类正确分类的样本数量之和除以总样本数；

$p_{e}$ 代表机遇符合率，计算方法为假设第一个人判断每一类的样本个数分别为a1,a2,…,aC，而第二个人判断每一类的样本个数分别为b1,b2,…,bC，总样本个数为n，则 $\mathrm{pe}=\frac{\mathrm{a} 1 \times \mathrm{b} 1+\mathrm{a} 2 \times \mathrm{b} 2+\ldots+\mathrm{aC} \times \mathrm{bC}}{\mathrm{n} \times \mathrm{n}}$ 。解释这一公式的来源，我们把分母中的一个n除到分子中，则每一个加和部分都除以n，以第一类为例 $\frac{\mathrm{a} 1 \times \mathrm{b} 1}{\mathrm{n}}$ ，将n除给a1，即第一个人判断所有人中有(a1/n)比例的人是属于第一类的，如果他是不受专业限制的随机判断，他也会认为第二个人将b1个人分为第一类的人里有(a1/n)比例的人是属于第一类的，这样相乘我们得到 $\frac{\mathrm{a} 1 \times \mathrm{b} 1}{\mathrm{n}}$ ，也就是在随机判断的情况下两个人判断一致的个数。将所有类别中由于机遇判断一致的个数加和除以总样本数得到机遇符合率。

下文给出一个计算例子：

使用cohen kappa系数衡量分类精度

$P_{\circ}=\frac{(a+d)}{n}=\frac{22+11}{39}=0.8462$

$P_{\mathrm{e}}=\frac{\left(\frac{f_{1} \times g_{1}}{n}\right)+\left(\frac{f_{2} \times g_{2}}{n}\right)}{n}=\frac{\left(\frac{26 \times 24}{39}\right)+\left(\frac{13 \times 15}{39}\right)}{39}=0.5385$

$\kappa=\frac{P_{\mathrm{o}}-P_{\mathrm{e}}}{1-P_{\mathrm{e}}}=\frac{0.8462-0.5385}{1-0.5385}=0.67$

Weighted Kappa

对于有序分类变量的一致性检验应该使用加权kappa系数。当分类类别代表等级分类，例如对疾病严重程度给出诊断，分为最轻到最重的五个等级。我们通常会认为，对同一个诊断的分级差异越大则造成的结果越严重，不一致性越强。例如将一个疾病最重的人判别为最轻和将一个疾病较轻的人判断为最轻带来的惩罚应该是不一样的。加权kappa便是基于这个思想。

线性加权(linear weighted kappa)认为每两个级别之间的差异相等，如果两个判定结果之间差三个类别，那么他们之间的不一致程度刚好是差一类的三倍，权值计算公式如下，其中i,j代表类别编号，其差值也就代表两个类别的距离。N为类别总数。由公式可知，判定结果一致时，权值为0。

$w_{i, j}=\frac{i-j}{N-1}$

平方加权(quadratic weighted kappa)则将线性加权的权值平方，放大级别距离大的判定不一致程度，权值计算公式如下：

$w_{i, j}=\frac{(i-j)^{2}}{(N-1)^{2}}$

kappa系数计算公式如下：

$\kappa=1-\frac{\sum_{i, j} w_{i, j} O_{i, j}}{\sum_{i, j} w_{i, j} E_{i, j}}$

其中 $O_{i, j}$ 代表将第i类判别为第j类的个数， $E_{i, j}$ 代表根据真实列联表根据上文提到的计算方法，计算机遇判断将会得到怎样的结果。其实就是对列联表中的所有值加权求和。

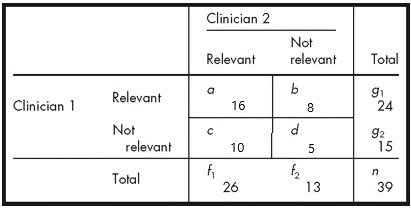
比如计算上文例子的线性加权kappa

$\sum_{i, j} w_{i, j} O_{i, j}=0\times22+1\times2+1\times4+0\times11=6$

计算机遇判断后得到的列联表如下

使用cohen kappa系数衡量分类精度

$\sum_{i, j} w_{i, j} E_{i, j}=0\times16+1\times8+1\times10+0\times5=18$

$\kappa=1-\frac{6}{18}=0.67$

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://yundeesoft.com/14950.html

使用cohen kappa系数衡量分类精度

Simple Kappa

Weighted Kappa

相关推荐

发表回复