大家好,欢迎来到IT知识分享网。
一、熵
熵的定义:
其对数log的底为2,若使用底为b的对数,则记为。当对数底为
时,熵的单位为奈特。
用表示数学期望,如果
,则随机变量
的期望值为,
当,
关于
的分布自指数学期望。而熵为随机变量
的期望值,其
是
的概率密度函数,则可写为,
引理:
证明:
二、联合熵与条件熵:
对于服从联合分布为的一对离散随机变量
,
联合熵的定义:
若,条件熵的定义:
定理链式法则:
证明:
等价记为:
推论:
,但
。
三、相对熵与互信息
两个概率密度函数为和
之间的相对熵或Kullback-Leibler距离定义为,
定义 考虑两个随机变量和
,它们的联合概率密度函数为
,其边际概率密度函数分别是
和
。
互信息为联合分布
和乘积分布
之间的相对熵,
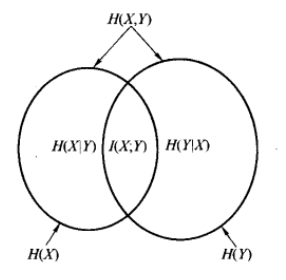
四、熵和互信息的关系
还可以将互信息写为,
由此可以看出,互信息是在给定
知识条件下
的不确定度的缩减量。则,
,联系到前面的
,可得,
最后得出,
因此,随机变量与自身的互信息为该随机变量的熵。有时,熵称为自信息就是这个原因。
熵和互信息的关系如下,
五、熵、相对熵与互信息的链式法则
一组随机变量的熵等于条件熵之和。
定理 设随机变量服从
,则
证明一:
证明二,由
可得:
给定时由于
的知识而引起关于
的不确定度的缩减量,即条件互信息的定义:
定理 互信息的链式法则:
证明:
条件相对熵的定义:
定理 相对熵的链式法则:
证明:
原文链接:熵、相对熵与互信息
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/23757.html