位运算与MOD快速幂详细知识点

大家好，欢迎来到IT知识分享网。

最近写的一些题目设计到了数论的取模

如下题

链接：https://ac.nowcoder.com/acm/contest/3003/G
来源：牛客网

题目描述

　　牛可乐有七个整数 a,b,c,d,e,f,g.并且他猜想a^d +b^e+c^f =g 但是牛可乐无法进行如此庞大的计算。请验证牛可乐的猜想是否成立。

 输入描述:

　　第一行一个正整数 T，表示有 T 组数据。
　　每组数据输入一行七个整数a,b,c,d,e,f,g 。
　　保证 1≤T≤1000 , −10⁹≤a,b,c,g≤10⁹, 0≤d,e,f≤10⁹ 保证不会出现指数和底数同为 0 的情况。

输出描述:

    每组数据输出一行，若猜想成立，输出 Yes ，否则输出 No。

示例：

　　输入：

　　　　2
　　　　1 1 4 5 1 4 258
　　　　114514 1919810 1 2 3 4 1

　　输出：

　　　　Yes
　　　　No

　　说明：

　　　　1⁵+1¹+4⁴=258
　　　　114514²+1919810³+1⁴ ≠ 1

这一题设计数论中的取模知识，现实运用则是快速幂（这题就是快速幂的模板题），然后快速幂就涉及位运算，所以此文就以此题为扩展，浅谈MOD运算快速幂与位运算。

当然这题直接暴力也行，但主要学习快速幂，先给暴力再标程（这个是提交记录里找的一个河南理工学长的代码（学长一直在更改代码提交，等等再研究他在思考什么），看了感觉他的代码长度较短，易懂，运行时间很短，内存占据较少，学长主页：https://ac.nowcoder.com/acm/contest/profile/287389065）

　　暴力：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int main(){
 4     long long n,a,b,c,d,e,f,g;
 5     cin>>n;
 6     while(n--){
 7         cin>>a>>b>>c>>d>>e>>f>>g;
 8         long long x=pow(a,d),y=pow(b,e),z=pow(c,f);
 9         if(x+y+z==g)cout<<"Yes"<<endl;
10         else cout<<"No"<<endl;
11     }
12     return 0;
13 }

　　快速幂：

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 const int mod=252585;
 5 ll qk(ll a,ll b)
 6 {
 7     ll res=1;
 8     while(b)
 9     {
10         if(b&1) res=res*a%mod;
11         a=a*a%mod;
12         b>>=1;
13     }
14     return res;
15 }
16 int main()
17 {
18     int t;
19     cin >>t;
20      
21     while(t--)
22     {
23         ll a,b,c,d,e,f,g;
24         cin >>a>>b>>c>>d>>e>>f>>g;
25         if(((qk(a,d)+qk(b,e))%mod+qk(c,f))%mod==g%mod) cout <<"Yes"<<endl;
26         else cout <<"No"<<endl;
27     }
28      
29 }

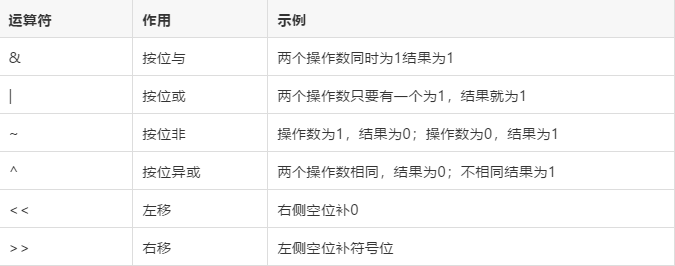
位运算：

　　基本运算符：

　　‘&’  实际运用：

　　　　（1）判断奇偶

　　　　　　因为二进制中偶数最后一位必定是0，奇数必定是1，所以对对一个数进行&运算等价于%=2

　　　　（2）清零

　　　　　　    若想对一个存储单元清零，即使其全部二进制位为0，只要找一个二进制数，其中各个位符合一下条件：
　　　　　　原来的数中为1的位，新数中相应位为0。然后使二者进行&运算，即可达到清零目的。

　　　　例：

　　　　　　66（10）= 01000010（2）

　　　　　　189（10） = 10111101（2）

　　　　　　则 66&189 = 0

 　　　　（3）取一个数中某些特定位

　　　　　　　　若有一个整数a(2byte),想要取其中的低字节，只需要将a与8个1按位与即可。
　　　　　

　　　　（4）保留指定位

　　　　　　　　例如：有一数84，即01010100（84），想把其中从左边算起的第3，4，5，7，8位保留下来，运算如下：

　　‘ | ’  实际运用：

 　　　　更改指定位置为1

　　　　　　例：如果想使一个数a的低4位改为1，则只需要将a与17（8）进行按位或运算即可。

 　　‘ ^ ’实际运用

　　　　(1)GCD快速求解

1 int GCD(int a,int b){
2     while(b^=a^=b^=a%=b);  //与a,b大小顺序无关
3     return a;
4 }

　　　　(2)使特定位翻转

　　　　　　设有数01111010（2），想使其低4位翻转，即1变0，0变1.可以将其与00001111（2）进行“异或”运算，即：

　　　　　　运算结果的低4位正好是原数低４位的翻转。可见，要使哪几位翻转就将与其进行∧运算的该几位置为１即可。

 　　　　（3）与0相“异或”，保留原值

　　　　　　　　例如：012^00=012

 　　　　　　因为原数中的1与0进行异或运算得1，0^0得0，故保留原数。

　　　　(4)交换两个值，不用临时变量

　　　　例如：ａ＝3，即 1|1|（2)；ｂ＝４，即1|0|0（2）。
　　　　　　想将ａ和ｂ的值互换，可以用以下赋值语句实现：
　　　　　　ａ＝a^b;
　　　　　　ｂ＝b^a;
　　　　　　ａ＝a^b;
　　　　　　ａ＝011(2)
　　　　　　（^）ｂ＝100(2)
　　　　　　ａ＝111(2)（a^b的结果，a已变成７）
　　　　　　（^）ｂ＝100(2)
　　　　　　ｂ＝011(2)（b^a的结果，b已变成３）
　　　　　　（^）ａ＝111(2)
　　　　　　ａ＝100（2）（a^b的结果，a已变成４）

　　　　　　–等效于以下两步：
　　　　　　① 执行前两个赋值语句：“ａ＝ａ^ｂ；”和“ｂ＝ｂ^ａ；”相当于b=b^(a^b)；
　　　　　　② 再执行第三个赋值语句： ａ＝ａ^ｂ。由于a的值等于（ａ^ｂ），b的值等于（ｂ^ａ^ｂ），因此，相当于a=ａ^ｂ^ｂ^ａ^ｂ，即a的值等于ａ^ａ^ｂ^ｂ^ｂ，等于ｂ。

　　左右移实际运用：

　　　　左右移x相当于乘除2的x次（都是在未溢出的情况下）,为了更好理解以十进制数为例，12345类似左移为123450相当于乘10，右移则是1234相当于除以10.因为是位运算所以比单纯的乘除要快。

　　　　左移1位相当于该数乘以2，左移2位相当于该数乘以2*2＝4,15 << 2=60，即乘了4 。但此结论只适用于该数左移时被溢出舍弃的高位中不包含1的情况。
　　　　假设以一个字节（8位）存一个整数，若ａ为无符号整型变量，则ａ＝64时，左移一位时溢出的是0，而左移2位时，溢出的高位中包含1。

　　　　　　右移运算符是用来将一个数的各二进制位右移若干位，移动的位数由右操作数指定（右操作数必须是非负值），移到右端的低位被舍弃，对于无符号数，高位补0。对于有符号数，某些机器将对左边空出的部分用符号位填补（即“算术移位”），而另　　　　一些机器则对左边空出的部分用0填补（即“逻辑移位”）。

　　　　注意：
　　　　　　对无符号数,右移时左边高位移入0；对于有符号的值,如果原来符号位为0(该数为正),则左边也是移入0。如果符号位原来为1(即负数),则左边移入0还是1,要取决于所用的计算机系统。有的系统移入0,有的系统移入1。移入0的称为“逻辑移位”,即简单移　　　　位；移入1的称为“算术移位”。

　　　　例： a的值是八进制数113755，
　　　　　　a:1001011111101101 （用二进制形式表示）
　　　　　　a>>1: 0100101111110110 (逻辑右移时)
　　　　　　a>>1: 1100101111110110 (算术右移时)
　　　　

　　　　在有些系统中,a>>1得八进制数045766,而在另一些系统上可能得到的是145766。Turbo C和其他一些C编译采用的是算术右移,即对有符号数右移时,如果符号位原来为1，左面移入高位的是1。

MOD运算：

　　取余与取模还是有区别的，见 https://blog.csdn.net/coder_panyy/article/details/73743722

　　mod运算，即求余(取模)运算，是在整数运算中求一个整数 x 除以另一个整数y的余数的运算，且不考虑运算的商。在计算机程序设计中都有MOD运算，其格式为： mod(nExp1,nExp2)，即是两个数值表达式作除法运算后的余数。

　　给定一个正整数p，任意一个整数n，一定存在等式 ：

　　取模运算：a % p（或a mod p），表示a除以p的余数。

　　运算规则

　　　　模运算与基本四则运算有些相似，但是除法例外。其规则如下：

　　　　　　(a + b) % p = (a % p + b % p) % p （1）

　　　　　　(a – b) % p = (a % p – b % p) % p （2）

　　　　　　(a * b) % p = (a % p * b % p) % p （3）

　　　　　　a ^ b % p = ((a % p)^b) % p （4）

　　　　结合律：

　　　　　　((a+b) % p + c) % p = (a + (b+c) % p) % p （5）

　　　　　　((a*b) % p * c)% p = (a * (b*c) % p) % p （6）

　　　　交换律：

　　　　　　(a + b) % p = (b+a) % p （7）

　　　　　　(a * b) % p = (b * a) % p （8）

　　　　分配律：

　　　　　　(a+b) % p = ( a % p + b % p ) % p （9）

　　　　　　((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p （10）

　　　　重要定理：

　　　　　　若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)；（11）

　　　　　　若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c) (%p)；（12）

　　　　　　若a≡b (% p)，c≡d (% p)，则 (a + c) ≡ (b + d) (%p)，(a – c) ≡ (b – d) (%p)，(a * c) ≡ (b * d) (%p)；（13）

    a≡b (mod n)表示a与b对模n同余。

    “≡”是数论中表示同余的符号。即给定一个正整数n，如果两个整数a和b满足a-b能被n整除，即(a-b)modn=0，那么就称整数a与b对模n同余，记作a≡b(modn)，同时可成立amodn=b。

    *扩展资料

    同余理论常被用于数论中。最先引用同余的概念与符号者为德国数学家高斯。同余的主要性质如下：

    1、自反性：a≡a（mod m）。

    2、对称性：若a≡b（mod m）,则b≡a（mod m）。

    3、传递性： 若a≡b（mod m)，b≡c（mod m）, 则a≡c（mod m）。

快速幂：

　　首先推荐一篇博客，讲的非常透彻  https://blog.csdn.net/qq_19782019/article/details/85621386

　　所以这里简单搬运和演示

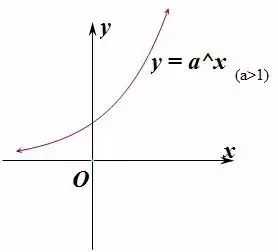
　　我们在初等数学中已知指数函数图像如下图：

　　那么在指数X超过某一值时，a^x 的值就开始急剧增长，以 → ∞，所以结果则会超过数据范围，因此我们需要结合MOD运算公式（公式（3）或者公式（4））对计算进行精确。

　　则此时的核心代码如下：

 1 /**  2  * 普通的求幂函数  3  * @param base 底数  4  * @param power 指数  5  * @return 求幂结果的最后3位数表示的整数  6 */  7 long long normalPower(long long base,long long power){  8 long long result=1;  9 for(int i=1;i<=power;i++){ 10 result=result*base; 11 result=result%1000; 12  } 13 return result%1000; 14 }

　　如果直接了当的求解pow(a,n)，那么时间复杂度为O（N），既N次循环。

　　那么快速幂的核心思想就是“遇奇则减，遇偶则方（“开方与平方”）”，如求3^10，则有以下路径：

3^10 = 9^5     //遇偶则方
9^5  = 9^4 * 9^1    //遇奇则减
9^4  = 81^2
81^2 = 6561^0 * 6561^1

那么 3^10 = 6561^0 * 6561^1 * 9^1 

 　　原本需要10次的算法，我们通过快速幂4次就算出了结果，由O(N) -> O(log N)

　　搬运上述博客模拟动图

 那么代码将变为：

 1 long long fastPower(long long base, long long power) {
 2     long long result = 1;
 3     while (power > 0) {
 4         if (power % 2 == 0) {
 5             //如果指数为偶数
 6             power = power / 2;//把指数缩小为一半
 7             base = base * base % 1000;//底数变大成原来的平方
 8         } else {
 9             //如果指数为奇数
10             power = power - 1;//把指数减去1，使其变成一个偶数
11             result = result * base % 1000;//此时记得要把指数为奇数时分离出来的底数的一次方收集好
12             power = power / 2;//此时指数为偶数，可以继续执行操作
13             base = base * base % 1000;
14         }
15     }
16     return result;
17 }

将语句简化：

 1 long long fastPower(long long base, long long power) {
 2     long long result = 1;
 3     while (power > 0) {
 4         if (power % 2 == 1) {
 5             result = result * base % 1000;
 6         }
 7         power = power / 2;
 8         base = (base * base) % 1000;
 9     }
10     return result;
11 }

结合位运算：

long long fastPower(long long base, long long power) {
    long long result = 1;
    while (power > 0) {
        if (power & 1) {//此处等价于if(power%2==1)
            result = result * base % 1000;
        }
        power >>= 1;//此处等价于power=power/2
        base = (base * base) % 1000;
    }
    return result;
}

所以得到模板：

 1 typedef long long ll;
 2 const ll mod=1e9+7;
 3 ll fastPower(ll base,ll power)
 4 {
 5     ll ans=1, res=base;
 6     while(power){
 7         if(power&1) ans=ans*res%mod;
 8         res=res*res%mod;
 9         power>>=1;
10     }
11     return ans%mod;
12 }

扩展递归写法：

　　注：不建议使用递归写法，容易超内存！

1 typedef long long ll;
2 const ll mod=1e9+7;
3 ll fastPower(ll m,ll n){   
4     if(n==1) return m;
5     int temp=fastPower(m,n>>1);
6     return (n&1? m%mod : 1)*temp*temp%mod;  //奇偶在此表现出差异
7 }