大家好,欢迎来到IT知识分享网。
有关凸包的知识其实并不难理解,稍微看看便可以懂得凸包的流程与原理。
1.什么是凸包?
在一个实数向量空间V中,对于给定集合X,所有包含X的凸集的交集S被称为X的凸包。(来源于百度百科)
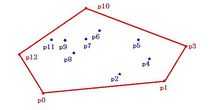
通俗来说,凸包便是可以将平面内所有点都包括进去的凸多边形。放张图理解一下,图中红色边框框起来的便是一个凸包。
2.怎么实现?
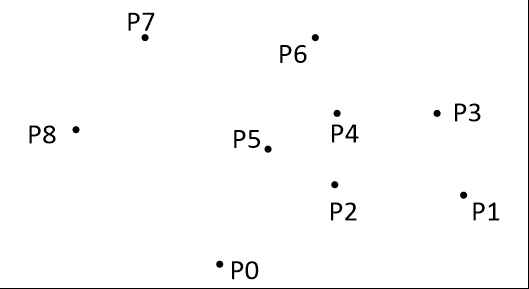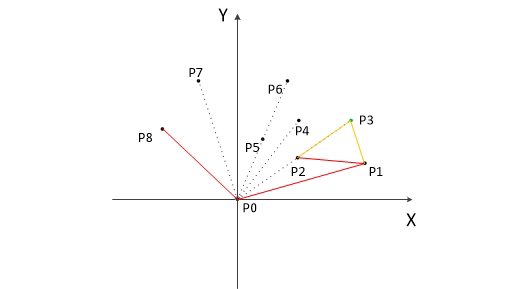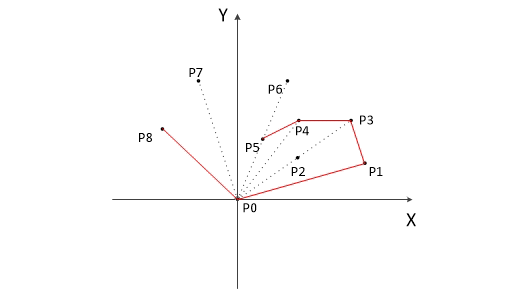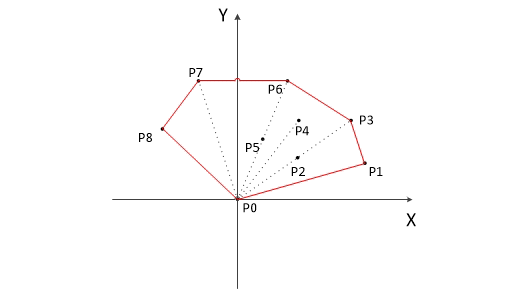
凸包的实现其实十分简单。先找出平面中最下面的点(即y坐标最下的点)u,这个点肯定在凸包上。再以这个点为极点进行极角排序。什么是极角排序呢,极角排序就是以点u为坐标原点,根据所有点与点u连成的直线与x轴正方向的夹角从小到大进行排序。极角排序后,将点u与夹角最小的点加入栈中,之后依次扫描每一个点,若这个点所处的位置在栈顶点的左边,则可以加入栈中,若在右边,就弹出栈首,如此扫描,最后凸包上的点就是栈中的元素。怎么判断扫描到的点在左边还是右边呢?这便要用到叉积的知识。设a(x1,y1),b(x2,y2),c(x3,y3),那么如果x1*y2+x2*y3+x3*y1>x1*y3+x2*y1+x3*y2,就可以说明点c在直线ab的右边(直线方向a->b)。
模板题:https://www.luogu.org/problemnew/show/P2742代码如下:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 #define rint register int 5 using namespace std; 6 7 struct node{ 8 double x,y; 9 }a[10001]; 10 int n,p,st[10001],top; 11 double ans,miny=2e9,minx=2e9; 12 13 int cmp(node b,node c) { //极角排序 14 if (fabs((b.y-miny)*(c.x-minx)-(c.y-miny)*(b.x-minx))<=1e-8) return fabs(minx-b.x)<fabs(minx-c.x); 15 return (b.y-miny)*(c.x-minx)<(c.y-miny)*(b.x-minx); 16 } 17 18 int check(int b,int c,int d) { //叉积判断 19 return ((a[b].x*a[c].y)+(a[c].x*a[d].y)+(a[d].x*a[b].y)-(a[b].x*a[d].y)-(a[c].x*a[b].y)-(a[d].x*a[c].y))>0; 20 } 21 22 double dist(double x1,double y1,double x2,double y2) { //计算两点间的欧几里得距离 23 return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); 24 } 25 26 int main() { 27 rint i; 28 scanf("%d",&n); 29 for (i=1;i<=n;++i) { 30 scanf("%lf %lf",&a[i].x,&a[i].y); 31 if (a[i].y<miny) { //寻找最下方的点 32 miny=a[i].y; minx=a[i].x; 33 } 34 } 35 sort(a+1,a+1+n,cmp); //极角排序 36 st[1]=1; st[2]=2; top=2; //将两个点加入栈中 37 for (i=3;i<=n;++i) { //扫描 38 while (!check(st[top-1],st[top],i)) top--; 39 st[++top]=i; 40 } 41 for (i=2;i<=top;++i) //计算答案 42 ans+=dist(a[st[i-1]].x,a[st[i-1]].y,a[st[i]].x,a[st[i]].y); 43 ans+=dist(a[st[top]].x,a[st[top]].y,a[1].x,a[st[1]].y); 44 printf("%.2lf",ans); 45 return 0; 46 }
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://yundeesoft.com/28406.html